yttuncel
- 28
- 0
Hello everybody,
I am stuck with a circuit that involves voltage controlled switch.
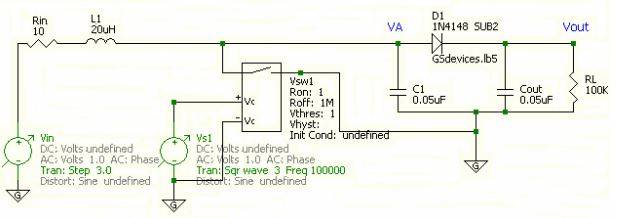
The switch is controlled with a square wave generator, Vs1, whose frequency is 100kHz. As far as I know, switch is off when source is on positive phase and vice versa. Therefore, I only need to compute Va when Vs1 is on negative phase, i.e. when the switch is on.
(When it is off, Va is grounded and Vout will decay to zero, however switch goes off before Vout decays. Therefore, me and my friend think that we can assume it to be constant.)
We assume diode is ideal. Then apply Node-Voltage analysis to node VA.
The node between inductor and Rin is called VB and iR is the current on Rin.
ic(t)=C\frac{dVc(t)}{dt} ... (1)
VL(t)=L\frac{diL(t)}{dt} ...(2)
When switch is on (when Va is not grounded),
iR=\frac{3-VB}{10}...(3)
With equations (1) and (3), the following is our Node-Voltage equation,
\frac{3-VB}{10}=0.05μ\frac{dVA}{dt}+0.05μ\frac{dVA}{dt}+\frac{VA}{100K}
and from (2) we have,
VB-VA=20μ\frac{diR}{dt}→VB=VA+20μ\frac{d\frac{3-VB}{10}}{dt}
Is this approach correct?
I mean, if I solve this system of DE, will I obtain the correct functions for node voltages when the switch is on?
Any help is appreciated :)
I am stuck with a circuit that involves voltage controlled switch.
Homework Statement
The switch is controlled with a square wave generator, Vs1, whose frequency is 100kHz. As far as I know, switch is off when source is on positive phase and vice versa. Therefore, I only need to compute Va when Vs1 is on negative phase, i.e. when the switch is on.
(When it is off, Va is grounded and Vout will decay to zero, however switch goes off before Vout decays. Therefore, me and my friend think that we can assume it to be constant.)
We assume diode is ideal. Then apply Node-Voltage analysis to node VA.
The node between inductor and Rin is called VB and iR is the current on Rin.
Homework Equations
ic(t)=C\frac{dVc(t)}{dt} ... (1)
VL(t)=L\frac{diL(t)}{dt} ...(2)
The Attempt at a Solution
When switch is on (when Va is not grounded),
iR=\frac{3-VB}{10}...(3)
With equations (1) and (3), the following is our Node-Voltage equation,
\frac{3-VB}{10}=0.05μ\frac{dVA}{dt}+0.05μ\frac{dVA}{dt}+\frac{VA}{100K}
and from (2) we have,
VB-VA=20μ\frac{diR}{dt}→VB=VA+20μ\frac{d\frac{3-VB}{10}}{dt}
Is this approach correct?
I mean, if I solve this system of DE, will I obtain the correct functions for node voltages when the switch is on?
Any help is appreciated :)
Last edited: