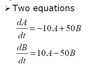Analytical solution of these coupled differential equations
- Thread starter gursimran
- Start date
Click For Summary
SUMMARY
The discussion focuses on solving coupled differential equations, specifically using techniques such as matrix exponentiation and decoupling. The user initially struggled with the problem but received guidance on differentiating the equations to derive a second-order differential equation for variable A. The solution emphasizes the importance of understanding eigenvalues and eigenvectors, as well as the application of matrix exponentiation in solving such equations. The discussion concludes with the user expressing gratitude for the simplified approach provided.
PREREQUISITES- Understanding of coupled differential equations
- Knowledge of matrix exponentiation
- Familiarity with eigenvalues and eigenvectors
- Ability to differentiate and manipulate differential equations
- Study the applications of matrix exponentiation in differential equations
- Learn how to decouple coupled differential equations
- Explore methods for finding eigenvalues and eigenvectors of matrices
- Practice solving second-order differential equations
Students and educators in mathematics, particularly those studying differential equations, as well as anyone seeking to improve their problem-solving skills in this area.
Similar threads
- · Replies 2 ·
- · Replies 21 ·
- · Replies 7 ·
- · Replies 25 ·
Undergrad
Solution To Photon Trajectory Equation
- · Replies 10 ·
- · Replies 4 ·
- · Replies 3 ·