Angle of Displacement of Rod Hit by Bullet in Time

[Gena]

Homework Statement

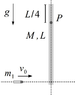
A rod of mass M y length L can spin freely around a fixed point P, as shown in the picture. A bullet of mass m is shot perpendicular to the rod, and after impact, it is embedded into it. After impact the system realizes small oscillations, and that immediately after impact, the bullet had a velocity Vo=5m/s.

Determine the expression that represents the evolution of the angle in radians tat the rod forms with respect to the vertical direction (measured counter-clockwise). The time t is measured in seconds once the impact occurs.
Data:
m=0.2kg
L=1.2m
M=1.5kg

Homework Equations

L=Iw
P=mv
I cm(rod)=(Ml²)/12

The Attempt at a Solution

I calculated the initial angular velocity of he rod by using the formulas written in relevant equations, but i don't know how to calculate the angle of displacement in time with that information. The fact that the bullet travels along with the rod after hitting it is really confusing as i don't know if the moment of inertia of the system changes.

 

[kuruman]

Your attempt at a solution is very sketchy. How did you apply the relevant equations? Specifically,
L=Iw: I assume this is the angular momentum relative to the pivot.
P=mv: This is not really useful here because momentum is not conserved since the rod is not free to move.
I cm(rod)=(Ml²)/12: This is the momentum of inertia relative to the CM. You need the expression relative to the pivot. After the bullet is embedded, you need to add its moment of inertia relative to the pivot.

Treat this as a physical pendulum the moment of inertia of which you can calculate. Use conservation of angular momentum to find the angular speed of the rod+bullet system after the collision is completed. The assumption here is that the bullet is embedded in the rod within a very short time interval and before the rod has a change to move appreciably.