Jason S
- 1
- 0
Member advised to use the homework template for posts in the homework sections of PF.
Hello everyone,
I am trying to figure out how to explain an aspect of this question to my students, but cannot seem to recall the geometry that explains the textbook's approach.
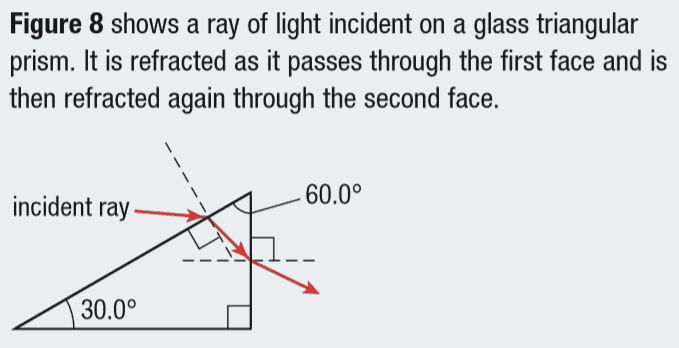
In the figure below, for part (b) of the question, we are using the angles of refraction at the left boundary to calculate the angles of incidence at the right boundary.
In the book, it states that if we use the angle of refraction at the left boundary, θ 2, and the angle of incidence at the right boundary, θ 3, then, according to the diagram, θ 2 + θ 3 = 60°, "which is the angle in the top right of the triangle".
I cannot, for the life of me, determine which relationship they are using to come to that conclusion.
This is the only aspect of this question that I need assistance with.
TIA.
Question:
Part B:

Textbook Solution:

I am trying to figure out how to explain an aspect of this question to my students, but cannot seem to recall the geometry that explains the textbook's approach.
In the figure below, for part (b) of the question, we are using the angles of refraction at the left boundary to calculate the angles of incidence at the right boundary.
In the book, it states that if we use the angle of refraction at the left boundary, θ 2, and the angle of incidence at the right boundary, θ 3, then, according to the diagram, θ 2 + θ 3 = 60°, "which is the angle in the top right of the triangle".
I cannot, for the life of me, determine which relationship they are using to come to that conclusion.
This is the only aspect of this question that I need assistance with.
TIA.
Question:
Part B:
Textbook Solution: