Angle relationships of a blazed diffraction grating

[NihalRi]

I am trying to understand how a blazed diffraction grating works and came across a deduction I don't understand. I believe that you don't need to know much about optics to answer this question as it is more geometry related.
I have the diagram below of a diffraction grating with all the relevant angles labeled.

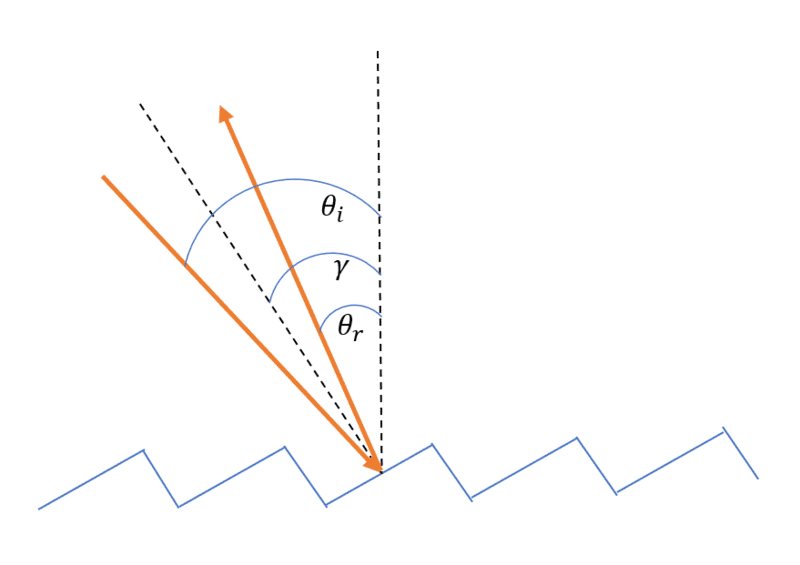
The blue zag is a zoom in of the diffraction grating surface. A beam (orange arrow on left) is hitting a face on the surfaces and reflecting (orange arrow on right) relative to normal of the face which is the dotted line between the arrows.
The deduction made is that θi - θr = 2γ and I can't seem to deduce this. I'll be happy to provide any additional information and any help will be appreciated.

 

[Charles Link]

$\theta_i-\gamma=\gamma-\theta_r$ for angle of incidence =angle of reflection (measured from the normal to the blaze). Simple algebra gives $\theta_i+\theta_r=2 \gamma$. The equation they have is in error, unless they assign an opposite sign to $\theta_r$. $\\$ (In some derivations, they do assign an opposite sign to $\theta_r$. The equation for constructive interference between adjacent slits or lines on a grating reads $m \lambda=d (\sin{\theta_i}\pm \sin{\theta_r} )$, (this is the condition/location for a primary maximum in the diffraction pattern), where the sign that is used in the $\pm$ depends upon the sign convention for how $\theta_r$ is measured. When they put in this opposite sign, this makes $\theta_i=\theta_r$ for $m=0$, so that the equation reads $m \lambda=d (\sin{\theta_i}-\sin{\theta_r} )$).

 

[NihalRi]

$\theta_i-\gamma=\gamma-\theta_r$ for angle of incidence =angle of reflection (measured from the normal to the blaze). Simple algebra gives $\theta_i+\theta_r=2 \gamma$. The equation they have is in error, unless they assign an opposite sign to $\theta_r$. $\\$ (In some derivations, they do assign an opposite sign to $\theta_r$. The equation for constructive interference between adjacent slits or lines on a grating reads $m \lambda=d (\sin{\theta_i}\pm \sin{\theta_r} )$, (this is the condition/location for a primary maximum in the diffraction pattern), where the sign that is used in the $\pm$ depends upon the sign convention for how $\theta_r$ is measured. When they put in this opposite sign, this makes $\theta_i=\theta_r$ for $m=0$, so that the equation reads $m \lambda=d (\sin{\theta_i}-\sin{\theta_r} )$).

Thank you, this makes perfect sense now!

 

[NihalRi]

$\theta_i-\gamma=\gamma-\theta_r$ for angle of incidence =angle of reflection (measured from the normal to the blaze). Simple algebra gives $\theta_i+\theta_r=2 \gamma$. The equation they have is in error, unless they assign an opposite sign to $\theta_r$. $\\$ (In some derivations, they do assign an opposite sign to $\theta_r$. The equation for constructive interference between adjacent slits or lines on a grating reads $m \lambda=d (\sin{\theta_i}\pm \sin{\theta_r} )$, (this is the condition/location for a primary maximum in the diffraction pattern), where the sign that is used in the $\pm$ depends upon the sign convention for how $\theta_r$ is measured. When they put in this opposite sign, this makes $\theta_i=\theta_r$ for $m=0$, so that the equation reads $m \lambda=d (\sin{\theta_i}-\sin{\theta_r} )$).

On another note, I'm likely to make this another thread but my aim is to uses the grating to combine two laser beams of different wavelengths. I want to do this in an energy efficient manner. Do you know any good resources I could use that explains the math of a blazed grating well?

 

[Charles Link]

On another note, I'm likely to make this another thread but my aim is to uses the grating to combine two laser beams of different wavelengths. I want to do this in an energy efficient manner. Do you know any good resources I could use that explains the math of a blazed grating well?

Your idea sounds like something that could work. Meanwhile I don't have any good source at present that discusses blazed gratings. You would need to google the topic. $\\$ For a blazed grating, the peak occurs when incident angle equals angle of reflection off of the blaze, but there is a spread of angles that can get a similar intensity, basically as a result of the single slit diffraction pattern width that occurs, as a multiplying factor of the multi-slit or multi-line interference result from the grating. See also: https://www.physicsforums.com/threa...ratio-of-power-densities.956805/#post-6066788 along with the "link" in post 7 of that thread which I will repeat here: http://www.physics.louisville.edu/cldavis/phys299/notes/lo_msgratings.html

 

[Charles Link]

@NihalRi Be sure and see the additions that I added to post 5 above.

 

[NihalRi]

Your idea sounds like something that could work. Meanwhile I don't have any good source at present that discusses blazed gratings. You would need to google the topic. $\\$ For a blazed grating, the peak occurs when incident angle equals angle of reflection off of the blaze, but there is a spread of angles that can get a similar intensity, basically as a result of the single slit diffraction pattern width that occurs, as a multiplying factor of the multi-slit or multi-line interference result from the grating. See also: https://www.physicsforums.com/threa...ratio-of-power-densities.956805/#post-6066788 along with the "link" in post 7 of that thread which I will repeat here: http://www.physics.louisville.edu/cldavis/phys299/notes/lo_msgratings.html

These look really helpful I will have a look into them. I had been reading that the Littrow configuration you mentioned had high efficiency. However wouldn't the order with the most energy be reflected back on the incidence beam and due to the conservation of energy the other orders be less intense?

 

[Charles Link]

These look really helpful I will have a look into them. I had been reading that the Littrow configuration you mentioned had high efficiency. However wouldn't the order with the most energy be reflected back on the incidence beam and due to the conservation of energy the other orders be less intense?

In general, (there are exceptions), the strongest portion of the emerging energy will not reflect back from where it originated. $\\$ I think you could even do what you are trying to do without a blazed grating. With an unblazed grating, the region with the highest energy will be such that the angle of incidence is approximately the angle of reflection. $\\$ You would simply take the two beams of interest and have them incident from reasonably close angles, and adjust the incident angles to get the primary maxima to coincide on the emerging beams. The emerging beams are most readily viewed by using a lens or paraboidal mirror to bring the beams to focus in the focal plane of the focusing optic. The beams will each focus to a point. The idea would be to get the focused points to coincide, by adjusting the incident angles. $\\$ Depending on the wavelengths that you have, you might have them be primary maxima of different orders $m$.

 

[Charles Link]

One additional tip for you on this project: In general, a typical laser is not collimated=it is a slightly diverging source. e.g. For a commercial type HeNe, it emerges from a small aperture and the beam spreads slightly with distance. If you want high precision in the focusing in the focal plane, it can be helpful to use optics to collimate the beams you are using. Alternatively, you can have them be far enough from the diffraction grating that the beam fills the grating. It will still tend to focus with $\frac{1}{f}=\frac{1}{b}+\frac{1}{m}$, but with $b$ quite large, the focus distance $m \approx f$.