Angular Movement and Spiralling Motion

[Cato11]

TL;DR

Moving on object in a collapsing spiral

Hello,

I am currently working on a computer program to move on object undergoing circular motion in a spiral of decreasing radius. I hope this is illustrated clearly below (forgive me but it is a sketch and thus not precise in scale):

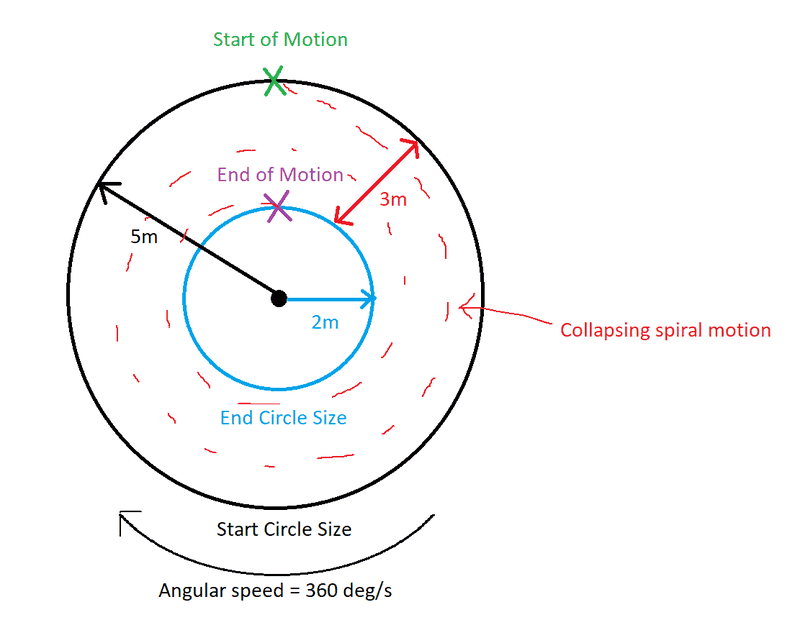
The scenario is as follows:

1. The object starts angular motion at the green "X"
2. The object starts orbiting at an angular speed of 360 deg/s
3. The object immediately undergoes the collapsing spiral when it starts moving from the green "X"
4. The spiral decreases at a linear (constant) rate
5. The object reaches the end of motion at the purple "X"

From this scenario, I can see that the linear distance covered is 3m. I also know that the angular speed (or velocity) is constantly changing during the spiral, since the radius is changing. The challenge I have is to control the exact number of spirals that occur between the green "X" and purple "X".

I have tried to tackle this challenge in multiple ways, but none of them are precise and I can never get an exact number of spirals - if I am aiming for say 2 spirals, sometimes it will overshoot and sometimes it will undershoot. I think my problem is that I am cobbling together code without understanding the underlying math, so I would really appreciate if anyone can advise how to achieve this in a precise and reliable way that is mathematically sound. A few of my initial thoughts are:

1. The linear distance must come into the equation somehow
2. I know what the start and end angular velocities are since I know the radii of the circles - this may be of some use

Any help would be greatly appreciated.

Thank you

 

[Ibix]

Well, if you know the angular velocity boils down to one revolution per second and you want $n$ revolutions then you need $n$ seconds, right? So if the difference in radii is $d$ then you need an inward radial speed of $d/n$. Unless there are other constraints on the path?

 

[Baluncore]

' spiral inwards
Const As Integer n = 2      ' number of turns
Dim As Double Ro = 5, Ri = 2    ' outer and inner radii

Const As Double TwoPi = 8 * Atn( 1 )
Dim As Double r, s, t, x, y, dt = ( Ro - Ri ) / n

For s = 0 To n Step 0.001
    r = Ro - ( s * dt )
    t = s * TwoPi
    x = r * Sin( t )    ' geographical coordinates
    y = r * Cos( t )
    Pset( x, y ), 14    ' points on the spiral
Next s

 

[jbriggs444]

What are you holding constant as you decrease the radius of the spiraling object?

Are you holding angular momentum constant? Are you holding rotation rate constant? Are you holding velocity constant? Or are you holding something else constant?

 

[Cato11]

Well, if you know the angular velocity boils down to one revolution per second and you want $n$ revolutions then you need $n$ seconds, right? So if the difference in radii is $d$ then you need an inward radial speed of $d/n$. Unless there are other constraints on the path?

I believe I made a mistake in my phrasing in the original post. It is the linear velocity that changes with radius (since v = wr). The angular velocity is at a constant 360 deg/s. I don't believe there are other constraints on the path. Do you know how to adjust the inward radial speed given this new information?

 

[Cato11]

What are you holding constant as you decrease the radius of the spiraling object?

Are you holding angular momentum constant? Are you holding rotation rate constant? Are you holding velocity constant? Or are you holding something else constant?

That is an excellent question! The angular momentum is being held constant and I have no control over it. I can however control the speed at which the object moves in towards the centre (whilst simultaneously orbiting at the constant angular momentum).

 

[jbriggs444]

That is an excellent question! The angular momentum is being held constant and I have no control over it. I can however control the speed at which the object moves in towards the centre (whilst simultaneously orbiting at the constant angular momentum).

So... just kind of mumbling to myself as I consider the problem.

You can "pull in the string" at any rate you please and you can thereby modulate the rate so that the spiral path takes on any (concave) shape that you please. You could, for instance, follow an Archimedes spiral and Google up the arc length for such a spiral.

Or do the same for an exponential spiral.

But perhaps I am not clear on what outputs your program is being asked to supply and what inputs it has access to along the way.

 

[Cato11]

So... just kind of mumbling to myself as I consider the problem.

You can "pull in the string" at any rate you please and you can thereby modulate the rate so that the spiral path takes on any (concave) shape that you please. You could, for instance, follow an Archimedes spiral and Google up the arc length for such a spiral.

Or do the same for an exponential spiral.

But perhaps I am not clear on what outputs your program is being asked to supply and what inputs it has access to along the way.

Your mumbling is very helpful as it is giving me food for thought, much appreciated!

I can access the following variables at any time but cannot change them:

- The angular speed (constant)
- The linear speed (v = wr)

I can change:

- The radius of the orbit and the speed at which it decreases

So effectively I need to nudge the orbiting body in towards the centre at just the right amount (or speed) such that it hits the end point (purple X) within a specified number of spirals. I hope it makes sense?

 

[jbriggs444]

I can access the following variables at any time but cannot change them:

- The angular speed (constant)
- The linear speed (v = wr)

If angular momentum is held constant then the angular speed cannot be held constant. Pick one.

The linear speed along the diagonal trajectory will be greater than the "horizontal" linear speed purely in the direction perpendicular to the line toward the center. $v=\omega r$ gives you the "horizontal" component of the velocity.

 

[Cato11]

If angular momentum is held constant then the angular speed cannot be held constant. Pick one.

The linear speed along the diagonal trajectory will be greater than the "horizontal" linear speed purely in the direction perpendicular to the line toward the center. $v=\omega r$ gives you the "horizontal" component of the velocity.

Okay so the angular speed is what is held constant, i.e. the object rotates at a fixed 360 deg/s.

 

[jbriggs444]

Okay so the angular speed is what is held constant, i.e. the object rotates at a fixed 360 deg/s.

Oh, then all you have to do is "reel in the string" at an even rate so that it takes time enough to hit the desired number of rotations, surely?

 

[Cato11]

Oh, then all you have to do is reel in the string at an even rate so that it takes time enough to hit the desired whole number of rotations, surely?

But how exactly do I find this rate? If I follow Ibix's suggestion, i.e. speed = difference in radii/number of turns, this does not produce the correct number of spirals. For example if I try 2 spirals, it will hit the smaller radius at approximately 1.7 spirals rather than 2. I also assume this loses precision as the number of spirals increases but that may not be the case.

 

[jbriggs444]

But how exactly do I find this rate? If I follow Ibix's suggestion, i.e. speed = difference in radii/number of turns, this does not produce the correct number of spirals. For example if I try 2 spirals, it will hit the smaller radius at approximately 1.7 spirals rather than 2. I also assume this loses precision as the number of spirals increases but that may not be the case.

If you want two rotations, then you need a reel-in rate of 1.5 meters per second. Over the course of two seconds, you will have two complete rotations around the center. What is the problem?

At a wild guess, you have decided to add up incremental diagonal arc length and divide by [current] altitude to get a cobbled-up angular rotation rate. You are then integrating that angular rotation rate to find that you've covered two complete rotations in only 1.7 seconds.

That would ignore the fact that 2 complete rotations take exactly 2 seconds given a 360 degree per second fixed rotation rate.

 

[Cato11]

If you want two rotations, then you need a reel-in rate of 1.5 meters per second. Over the course of two seconds, you will have two complete rotations around the center. What is the problem?

At a wild guess, you have decided to add up incremental diagonal arc length and divide by [current] altitude to get a cobbled-up angular rotation rate. You are then integrating that angular rotation rate to find that you've covered two complete rotations in only 1.7 seconds.

That would ignore the fact that 2 complete rotations take exactly 2 seconds given a 360 degree per second fixed rotation rate.

I understand your first point but the problem is that I am not seeing what is expected, i.e. by setting the reel-rate it does not complete the expected 2 full spirals.

I don't believe I am cobbling together the angular rotation rate, that is fixed at 360 deg/s. And I am not integrating anything, I am linearly interpolating the radius whilst the object moves, and it literally hits the smaller radius significantly before 2 full turns.

Perhaps there is something else going on that I need to investigate, I will do a careful inspection and hopefully report back soon. I really appreciate the help by the way so thank you for persisting with me.

 

[jbriggs444]

I understand your first point but the problem is that I am not seeing what is expected, i.e. by setting the reel-rate it does not complete the expected 2 full spirals.

I don't believe I am cobbling together the angular rotation rate, that is fixed at 360 deg/s. And I am not integrating anything, I am linearly interpolating the radius whilst the object moves, and it literally hits the smaller radius significantly before 2 full turns.

If you are updating the position and applying the wrong trig functions to do so, the result could be exactly the sort of incorrect result you report.

A bunch of small steps added together is practically the definition of integration.

 

[Baluncore]

4. The spiral decreases at a linear (constant) rate

Is each turn of the spiral equally spaced, the same distance from the previous turn ?

Use the code in post #3, or post your code that does not work.

 

[mewsli01]

Is each turn of the spiral equally spaced, the same distance from the previous turn ?

Use the code in post #3, or post your code that does not work.

 

[mewsli01]

You know the initial radius r you know initial angular acceleration therefore you know tangential velocity which should be constant throughout the spiral
You know the final radius r-d you know tangential velocity you calculate angular acceleration v=wr
How can you keep angular acceleration constant and reduce radius in a spiral at same time without some sort of force
It defeats law of physics