Angular Velocity Keeping Strings Taut

[newtophysics2]

Homework Statement

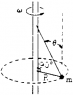
A ball of mass m is attached by two strings to a vertical rod. as shown in the diagram attached. The entire system rotates at constant angular velocity ω about the axis of the rod.

a)Assuming ω is large enough to keep both strings taut, find the force each string exerts on the ball in terms of ω, m, g, R, and θ.

b)Find the minimum angular velocity, θ_min for which the lower string barely remains taut.

Homework Equations

F_centripetal=mv²/r
F=ma

The Attempt at a Solution

A) To keep the strings taut, the net force in the y-axis and the x-axis have to both equal 0. I used forces and tension, but my answer didn't contain ω, but I feel like it should...
T1 tension is making θ angle with the vertical
T1cosθ along vertical upward
T1sinθ along horizental i.e towards the center of the circular path
applying ΣFy =0 ΣFx =0
T1cosθ=mg
T1=mg/cosθ
T1sinθ+T2=mv2/R
T2=mgsinθ+mv2/R

B) I would solve for v from the equations above, but the question doesn't say that I can use T (tension) in my answer...

What am I doing wrong in this problem? Thanks in advance!

 

[Spinnor]

Velocity and angular velocity are related by,

v = ωR

Also,

b)Find the minimum angular velocity, θ_min for which the lower string barely remains taut.

should read,

b)Find the minimum angular velocity, ω_min for which the lower string barely remains taut.

 

[newtophysics2]

Ok, thanks! So did I do part A correctly? And for part B, do I just set T2=0 and then substitute v=ωR to solve for ω?

 

[haruspex]

A) To keep the strings taut, the net force in the y-axis and the x-axis have to both equal 0.

No. The complete equation is F_net=ma. There is an acceleration, so the net force must provide that.

 

[newtophysics2]

No. The complete equation is F_net=ma. There is an acceleration, so the net force must provide that.

How do I determine the acceleration? So is my solution wrong?

 

[haruspex]

How do I determine the acceleration? So is my solution wrong?

You already correctly used it in your equations, here:

T1sinθ+T2=mv2/R

I was just pointing out that your comment that the net force in the x direction is 0 was wrong.

T1cosθ=mg
T1=mg/cosθ
T1sinθ+T2=mv²/R
T2=mgsinθ+mv²/R

I don't think that last equation follows from the ones before.
Also, part requires you to find the tensions in terms of ω, m, g, R, and θ, not v. So you need Spinnor's equation there..
For part B, yes, put T2 = 0 and find ω.