Angular velocity of a wheel rolling around a fixed axis

[sid0123]

Mentor note: Moved to homework section[/color]

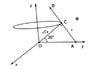
A conical wheel is rolling (without slipping) around a fixed axis OZ as shown in the figure. The velocity of point C is v_c = at.

The direction of the velocity of C is shown by a cross i.e. along negative x-axis.
We have to find the angular velocity, angular acceleration of the wheel and also the velocity and acceleration of point B.

Now, using the Euler's equation, we can write it as

v_a = v_o + ω x OA
As rolling is without slipping, v_a is 0 and v_o is also 0.

So, I got ω x OA = 0. That means that ω ιι OA. That means ω_x and ω_z are both zero.

Now, I used the Euler equation for point O and C,
v_c = v_o + ω_y X OC.

Solving this, I got ω_y = -2at/r√3

That means ω = (0) i + (-2at/r√3 ) j + (0) k

So, I got the angular velocity vector along negative y axis. I am confused that is this the angular velocity of the wheel with respect to its own axis, or the angular velocity of the entire wheel with respect the the central axis OZ or the net angular velocity considering the angular velocity around its own axis + angular velocity around the central axis OZ?

 

[TSny]

So, I got the angular velocity vector along negative y axis. I am confused that is this the angular velocity of the wheel with respect to its own axis, or the angular velocity of the entire wheel with respect the the central axis OZ or the net angular velocity considering the angular velocity around its own axis + angular velocity around the central axis OZ?

Consider separately the directions of the angular velocity $\vec \omega_1$ due to rotation about the axis of the cone and angular velocity $\vec \omega_2$ due to rotation of the cone around the z-axis. Do either of these two vectors point in the negative y direction? Is it possible for their sum to point in the negative y direction?

Your calculation looks correct to me. But note that it gives the angular velocity vector at the particular instant when the cone is touching the y axis. What about other instants of time?