rara
- 3
- 0
Gear C has radius 0.12 m and rotates with angular velocity 1.9 k rad/s. The connecting link rotates at angular velocity 1.5 k rad/s. Gear D has radius 0.05 m. Find the angular velocity of gear D (in rad/s). Note that gear C is pinned to ground and gear D is a planetary gear.
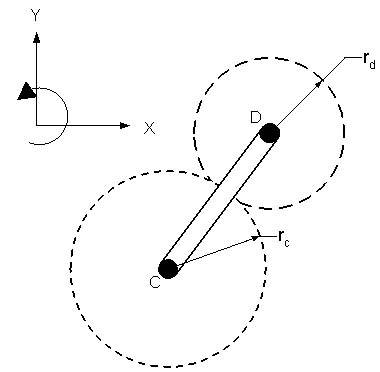
Since gear c is pinned, the gear ratio ωc/ωd=rd/rc does not directly apply here right? I wonder if the correct solution would be ωd=ωc x rcd / rd. I got -2.125 rad/s. Thanks.
Since gear c is pinned, the gear ratio ωc/ωd=rd/rc does not directly apply here right? I wonder if the correct solution would be ωd=ωc x rcd / rd. I got -2.125 rad/s. Thanks.