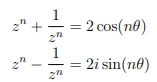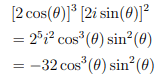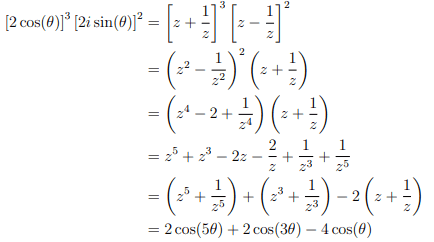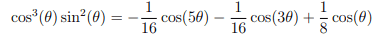SUMMARY
This discussion centers on the exploration of trigonometric identities, specifically the connection between complex exponentials and sinusoidal functions. Participants express gratitude for insights and share references to relevant articles that elucidate these concepts. The conversation highlights the importance of understanding these relationships in precalculus studies. The thread was eventually locked due to a related question being posted in the appropriate Precalc Homework section.
PREREQUISITES
- Understanding of trigonometric identities
- Familiarity with complex exponentials
- Basic knowledge of sinusoidal functions
- Precalculus concepts
NEXT STEPS
- Research the relationship between complex exponentials and trigonometric functions
- Study Euler's formula and its applications in trigonometry
- Explore advanced trigonometric identities and their proofs
- Review precalculus resources focusing on sinusoidal functions
USEFUL FOR
Students studying precalculus, educators teaching trigonometric identities, and anyone interested in the mathematical connections between complex numbers and trigonometric functions.