Application of the first law of thermodynamics

[abdossamad2003]

In Halliday's physics book, there is an example of the first law of thermodynamics that shows its application. The figure below explains this example:

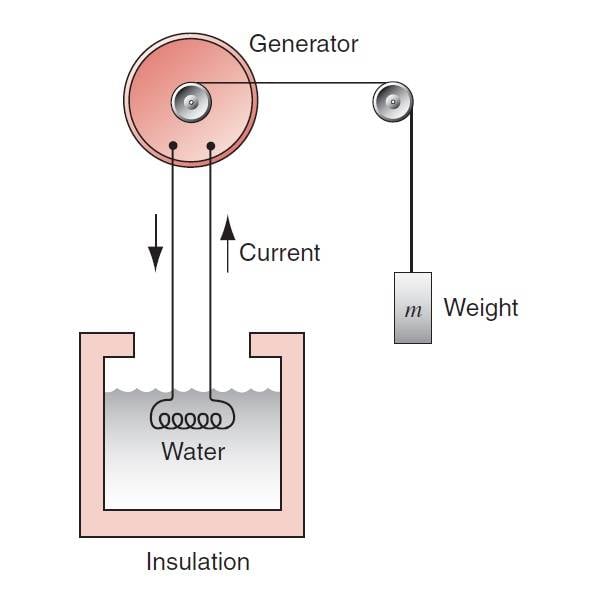
Here is a question, if the element alone is chosen as the system, doubts arise in the first law, because in this system, Q<0 (because heat is transferred from the element to the water) and W=0 (because there is no external work on the system is not done) as a result the internal energy of the system (the element alone) should decrease while it does not because the temperature of the element is constant.!!!Part of the text:

 

[Dale]

W=0 (because there is no external work on the system is not done)

There is external work done on the system (the resistor). The electrical work done is $$W=\int I(t)\ V(t) \ dt$$ Where $I$ is the current through the resistor and $V$ is the voltage across it.

 

[Chestermiller]

For the combination of weight and coil, external work is done by gravity on the weight (by the earth), as the weight lowers. An approximately equal amount of heat is delivered from the coil to the water. The book author is a little wrong, because the coil gets a little hotter as the water gets a little hotter. But this increase in internal energy of the coil is negligible compared to the increase in internal energy of the water. The assumption is that the velocity of the weight does not increase significantly during the test, so that its kinetic energy doesn't need to be accounted for.

 

[abdossamad2003]

There is external work done on the system (the resistor). The electrical work done is $$W=\int I(t)\ V(t) \ dt$$ Where $I$ is the current through the resistor and $V$ is the voltage across it.

I thought that in the first law of thermodynamics, W external mechanical work is not necessarily mechanical work and can be electrical work and so on.

 

[Dale]

I thought that in the first law of thermodynamics, W external mechanical work is not necessarily mechanical work and can be electrical work and so on.

Yes, the expression I wrote is the expression for electrical work. It is not zero.

 

[abdossamad2003]

My second question is, if the initial and final state are not in equilibrium, then the first law of thermodynamics is not correct. Can you give an example?

 

[Chestermiller]

My second question is, if the initial and final state are not in equilibrium, then the first law of thermodynamics is not correct. Can you give an example?

View attachment 334300

An example is a gas within an insulated cylinder, featuring a massless frictionless piston above, where a weight is sitting on top of the piston, and part of the weight is suddenly removed; the gas expands rapidly and irreversibly. All intermediate states are not thermodynamic equilibrium states, and the first law of thermodynamics can not be used to determine the internal energy for these states. It can only be used for the final state in which the gas is again at thermodynamic equilibrium.

 

[Squizzie]

An example is a gas within an insulated cylinder, featuring a massless frictionless piston above, where a weight is sitting on top of the piston, and part of the weight is suddenly removed; the gas expands rapidly and irreversibly. All intermediate states are not thermodynamic equilibrium states, and the first law of thermodynamics can not be used to determine the internal energy for these states. It can only be used for the final state in which the gas is again at thermodynamic equilibrium.

But in an ideal case, wouldn't the piston oscillate indefinitely, as PE and KE are exchanged cyclically as the piston moves up and down under the influence of the pressure in the cylinder?

 

[Chestermiller]

But in an ideal case, wouldn't the piston oscillate indefinitely, as PE and KE are exchanged cyclically as the piston moves up and down under the influence of the pressure in the cylinder?

No. Even in the ideal gas limit, gases exhibit viscous behavior which would act to damp the oscillation. See Transport Phenomena by Bird, Stewart, and Lightfoot, Chapter 1, Section 1.3 Temperature and Pressure Dependence of Viscosity and Fig. 1.3-1. Viscous behavior will prevail as long as the mean free path of the molecules is small compared to the physical dimensions of the system (e.g., the piston diameter).

Viscous stresses are also the reason why the ideal gas law cannot be used for rapidly deforming irreversible deformations. In such cases, even though the gas may exhibit ideal gas behavior at thermodynamic equilibrium (and in reversible deformations, which are always comprised of a continuous sequence of thermodynamic equilibrium states), in irreversible deformations, the ideal gas does not exhibit ideal gas behavior (except in the initial- and final thermodynamic equilibrium states).

 

[Squizzie]

No. Even in the ideal gas limit, gases exhibit viscous behavior

But doesn't "ideal" require an ideal gas: one that obeys PV=nRT over all ranges of temperature and pressure, with no viscosity?

 

[Chestermiller]

But doesn't "ideal" require an ideal gas: one that obeys PV=nRT over all ranges of temperature and pressure, with no viscosity?

No. An ideal gas is the limit of real gas behavior at low pressures (but not so low that the mean free path of the molecules is on the same order or larger than the physical dimensions of the system). Bird, et al. state "The chart (Fig. 1.3-1) shows that the viscosity of a gas approaches a limit (the low density limit) as the pressure becomes smaller; for most gases, this limit is nearly attained at 1 atm. pressure."

Because of viscosity, an ideal gas obeys PV=nRT only at thermodynamic equilibrium.

 

[Squizzie]

No. An ideal gas is the limit of real gas behavior at low pressures (but not so low that the mean free path of the molecules is on the same order or larger than the physical dimensions of the system). Bird, et al. state "The chart (Fig. 1.3-1) shows that the viscosity of a gas approaches a limit (the low density limit) as the pressure becomes smaller; for most gases, this limit is nearly attained at 1 atm. pressure."

Because of viscosity, an ideal gas obeys PV=nRT only at thermodynamic equilibrium.

I think you'll find that Bird, et al. were referring to the viscosity of a real gas, not an ideal gas.
Tuckerman refers to an ideal gas as "an ideal gas, which is defined (thermodynamically) as a system whose equation of state is PV − nRT = 0,"
and "An ideal gas is defined to be a system of particles that do not interact."

 

[Chestermiller]

I think you'll find that Bird, et al. were referring to the viscosity of a real gas, not an ideal gas.
Tuckerman refers to an ideal gas as "an ideal gas, which is defined (thermodynamically) as a system whose equation of state is PV − nRT = 0,"
and "An ideal gas is defined to be a system of particles that do not interact."

Well, with all due respect to Tuckerman (whoever that is), you are not going to be able to explain mechanistically what happens in Joule expansion in a rigid container, or Joule Thomson change in flow through a porous plug or valve, or Joule heating by an impeller without taking into account the viscous behavior of the gas.

I guess we are just going to have to agree to disagree.

 

[Squizzie]

Well, with all due respect to Tuckerman (whoever that is),

Tuckerman, Mark E. (2010). Statistical Mechanics: Theory and Molecular Simulation (1st ed.). ISBN 978-0-19-852526-4.

 

[Chestermiller]

Tuckerman, Mark E. (2010). Statistical Mechanics: Theory and Molecular Simulation (1st ed.). p. 87. ISBN 978-0-19-852526-4.

Statistical Mechanics?? That applies only to thermodynamic equilibrium conditions, and we have been considering here irreversible processes in which the system passes through non-equilibrium states (not described by statistical mechanics). How does statistical mechanics treat irreversible processes. And when molecular simulation is done, this has to take into consideration molecular interactions. But, as you said (which I disagree with), An ideal gas is defined to be a system of particles that do not interact." So how can statistical mechanics deal with particles that do not interact (and yet describe an irreversible process for such a system)?

 

[Squizzie]

Statistical Mechanics??

Young and Friedman (2018) University Physics with Modern Physics, 15th Edition Sears & Zemansky

 

[Chestermiller]

View attachment 335199
Young and Friedman (2018) University Physics with Modern Physics, 15th Edition Sears & Zemansky

Only for thermodynamic equilibrium!

 

[Squizzie]

Only for thermodynamic equilibrium!

If that is the case, then if along with assuming the "ideal" states of an insulated cylinder and a massless, frictionless piston, we assume that the gas is an ideal gas, how should we model your example?

An example is a gas within an insulated cylinder, featuring a massless frictionless piston above, where a weight is sitting on top of the piston, and part of the weight is suddenly removed; the gas expands rapidly and irreversibly.

And why is the expansion of the gas "irreversible"?

 

[Chestermiller]

If that is the case, then if along with assuming the "ideal" states of an insulated cylinder and a massless, frictionless piston, we assume that the gas is an ideal gas, how should we model your example?

Which example is that?

And why is the expansion of the gas "irreversible"?

Do you understand how an irreversible process is defined. Please articulate your understanding.

 

[Squizzie]

Which example is that?

Your example at #7:

An example is a gas within an insulated cylinder, featuring a massless frictionless piston above, where a weight is sitting on top of the piston, and part of the weight is suddenly removed; the gas expands rapidly and irreversibly.

Do you understand how an irreversible process is defined. Please articulate your understanding.

You stated in the example that the process was irreversible. It seemed to me that, by specifying an insulated cylinder and frictionless piston, you had specified purely adiabatic process. My question was requesting an explanation of why (or more accurately, how?) the described process would be irreversible.

 

[Squizzie]

Just for giggles, I have simulated the example in python and have run it for an initial mass of 10 tonnes, removing 1 tonne :

Interesting things happen when most of the weight is removed. Here's removing 9,800 kg (all but 100 kg) and running the simulation for 30,000 iterations:

I think the process is reversible.

""" "An example is a gas within an insulated cylinder, featuring a massless frictionless piston above, where a weight is sitting on top of the piston, and part of the weight is suddenly removed." Modelling: The cylinder has a cross-section of 1 metre The initial weight is 1 tonne. There is sufficient quantity of gas to support the pistom 1 metre from the base, giving an initial gas volume of 1 cubic metre. A mass (coded as deltaM below) is suddenly removed. A numerical solution """ import numpy as np import matplotlib.pyplot as plt g = 9.8 # m/sec^2 Gravity. gamma = 1.4 # the adiabatic index of air M = 10000 # kg Initial mass deltaM = 1000 # kg, mass removed newMass = M - deltaM gf = newMass * g # kilo newtons gravitational force of new mass step = 0.0010 # seconds. The time interval for the iteration time_steps = 10000 # the number of iterations time = np.linspace(0, step * time_steps, time_steps) xPosition = np.zeros(time_steps) #the array of x-values at each time interval def oscillatePiston(): for i in range(time_steps): if i == 0: # initial conditions initialForce = M * g # initial pressure force from 1 cu metre compressed with the initial mass. netForce = initialForce - gf x=1 # meters. start position v=0 # initial velocity m/sec else: v1 = v + a * step # m/sec x = x + (v1 + v) / 2 * step # use the average of previous and current velocity to calculate the next position pf = initialForce * (x**(-gamma)) # The volume is proportional to the value of x pressure force netForce = pf - gf # net force on piston is weight of the mass minus the pressure force of the gas. v = v1 # set v for next iterations a = netForce / newMass # acceleration (force = mass * acceleration) xPosition[i] = x oscillatePiston() plt.plot(time, xPosition) plt.xlabel('Time (seconds)') plt.ylabel('Position (meters)') plt.title('Piston Oscillation') plt.show()

 

[Chestermiller]

Your example at #7:

I'll present a. solution to that after you answer my question about your understanding of the definition of an irreversible process.

You stated in the example that the process was irreversible. It seemed to me that, by specifying an insulated cylinder and frictionless piston, you had specified purely adiabatic process. My question was requesting an explanation of why (or more accurately, how?) the described process would be irreversible.

Again, what is your definition of an irreversible process?

 

[Squizzie]

Again, what is your definition of an irreversible process?

I assumed that you were referring to the standard thermodynamics interpretation of an irreversible process. Here's one from Cengel Y. A. and Boles M. A.(2015) Thermodynamics: An Engineering Approach McGraw Hill p. 292:
"A reversible process is defined as a process that can be reversed without leaving any trace on the surroundings (Fig. 6–29). That is, both the system and the surroundings are returned to their initial states at the end of the reverse process. This is possible only if the net heat and net work exchange between the system and the surroundings is zero for the combined (original and reverse) process. Processes that are not reversible are called irreversible processes."

 

[Chestermiller]

I have n moles of gas inside an insulated cylinder of area A sitting in a vacuum chamber, with its axis oriented vertically. The piston is frictionless and massless, but there is initially a mass M sitting on top of the piston, so that the initial pressure of the gas is $P_1=\frac{Mg}{A}$; the initial. temperature is $T_1$. I suddenly remove mass m<M from the top of the piston, and let the gas expand and re-equilibrate so that its final pressure is $P_2=\frac{(M-m)g}{A}$. Since viscous forces will damp the motion of the mass during the process, and it will eventually come to rest. Use the 1st law of thermodynamics to determine the final temperature.

In this process, the total amount of work done by the gas in lifting the weight is $$W=(M-m)g\Delta h=\frac{(M-m)g}{A}(V_2-V_1)=P_2(V_2-V_1)$$Combining this with the ideal gas law gives:$$W=nRT_2-P_2\frac{nRT_1}{P_1}=nR\left(T_2-\frac{P_2}{P_1}T_1\right)$$For an. ideal gas, the change in internal energy is $$\Delta U=nC_v(T_2-T_1)$$ so that $$nC_v(T_2-T_1)=-nR\left(T_2-\frac{P_2}{P_1}T_1\right)$$Solving for the final equilibrium temperature $T_2$ gives $$T_2=\frac{C_v+R(P_2/P_1)}{C_p}T_1$$
Questions?

If this were a reversible process, since the system is adiabatic, the change in entropy would be zero.

 

[Squizzie]

Questions?

Is your gas an ideal gas?

 

[Chestermiller]

Is your gas an ideal gas?

Did I use the ideal gas law and the equation for the internal energy of an ideal gas?

 

[Squizzie]

Did I use the ideal gas law and the equation for the internal energy of an ideal gas?

Yes, you did use the ideal gas law in

For an. ideal gas, the change in internal energy is $$\Delta U=nC_v(T_2-T_1)$$

So I think it's a fair question: Is your gas an ideal gas?

 

[Chestermiller]

What do you think?

 

[Squizzie]

What do you think?

I think it's a pretty straightforward question. Is your answer modelled on an ideal gas?

 

[Chestermiller]

I think it's a pretty straightforward question. Is your answer modelled on an ideal gas?

Do you think I did?

 

[Squizzie]

Do you think I did?

I'm just asking a simple question about a detail about your example which is quite significant to the understanding of your explanation.

 

[Chestermiller]

I'm just asking a simple question about a detail about your example which is quite significant to the understanding of your explanation.

It is an ideal gas according to the definition of an ideal gas used by chemical engineers.

 

[vanhees71]

Statistical Mechanics?? That applies only to thermodynamic equilibrium conditions, and we have been considering here irreversible processes in which the system passes through non-equilibrium states (not described by statistical mechanics). How does statistical mechanics treat irreversible processes. And when molecular simulation is done, this has to take into consideration molecular interactions. But, as you said (which I disagree with), An ideal gas is defined to be a system of particles that do not interact." So how can statistical mechanics deal with particles that do not interact (and yet describe an irreversible process for such a system)?

I think, Boltzmann would be pretty sad, hearing this. Of course statistical mechanics is by no means restricted to thermostatics.

 

[Chestermiller]

I think, Boltzmann would be pretty sad, hearing this. Of course statistical mechanics is by no means restricted to thermostatics.

So how would Boltzmann have handled a specific problem involving an irreversible process between an initial and final thermodynamic equilibrium state. Please provide an example with details.

 

[vanhees71]

You mean the problem described in #1? I guess, he'd solve the equation of motion for $m$ together with the AC circuit problem. Then the total energy consumed in the resistor is transferred to the water as heat. I don't see, where in this entire problem an ideal gas occurs in the first place.