mahela007
- 105
- 0
Homework Statement
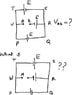
Find the Voltage across A B in the following circuit. Each cells has negligible internal resistance and an EMF of E volts.
(First diagram in the attached picture)
Homework Equations
I'm trying to use Kirchoff's second law.
The Attempt at a Solution
Now, if I traverse the RSTU loop in the clockwise direction, I find that VAB = 2E.
Similarly, if I traverse the loop RQPU, I also get VAB = 2E.
In this case, traversing either loop gives the same answer for VAB
But what if the polarity of cell TS (the top most cell) was reversed as in the second diagram?
In this case, applying Kirchoff's law to loops RSTU and RQPU yields different results for VAB.. so in such a case, what is the actual value of VAB