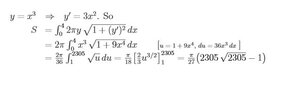SUMMARY
The discussion centers on the process of changing the limits of integration in a definite integral when making a substitution. The substitution used is defined as u(x) = 1 + 9x^4, which transforms the limits from 0 to 4 into new limits of 1 to 2305. The calculation shows that u(0) = 1 and u(4) = 2305, confirming the correct application of the substitution method in integral calculus.
PREREQUISITES
- Understanding of definite integrals
- Familiarity with substitution methods in calculus
- Knowledge of how to compute limits of integration
- Basic algebraic manipulation skills
NEXT STEPS
- Study the process of variable substitution in integrals
- Learn about the Fundamental Theorem of Calculus
- Explore advanced integration techniques, such as integration by parts
- Practice problems involving changing limits of integration
USEFUL FOR
Students and educators in calculus, mathematicians focusing on integration techniques, and anyone looking to deepen their understanding of definite integrals and substitution methods.