Are energy levels in a Debye solid equivalent to particles?

[Karthiksrao]

Dear all,

In the wiki article about Debye solid :
https://en.wikipedia.org/wiki/Debye_model , in the section 'Another derivation', below Eq. 6, the following statement is provided:

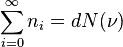
Here, I understand the right hand side, which is nothing but the density of states/modes at the frequency \nu.

I fail to understand how this can be equated to the total number of photons (particles) Sigma n_i

Is each mode/state equivalent to a particle ?

Thanks!

 

[nasu]

It's not the total number of phonons but just the total number of phonons with frequency $\nu$. For a given frequency you can have different energies associated (E_i) and for each energy level you have some number of phonons (n_i).

 

[Karthiksrao]

oh yes, I did actually have in mind total number of photons with frequency \nu.

So just to clear things up, at every frequency \nu, there are many energy levels corresponding to 1 h \nu, 2 h \nu, 3 h \nu, etc.
Each of these energy levels is populated by photons. If you add up the number of photons distributed in all these energy levels, I am unable to visualize why this sum comes out to be just equal to the number of energy levels at frequency \nu (or the density of states at frequency \nu) represented by dN(\nu) in the expression. Can't each energy level hold more than one photon ? That doesn't seem right.