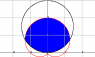
ex81
- 73
- 0
Homework Statement
find the over lapping area of the following equations
r=3sin(x)
r=1+sin(x)
Homework Equations
area =1/2 ∫ f(x)^2 dx
The Attempt at a Solution
first off I started by finding the intersecting angle by:
3sin(x)=1+sin(x)
2sin(x)=1
sin(x)=1/2
x=pi/6
and the peak is at pi/2
so I started with a = 2×1/2 ∫ (1+sin(x))^2 dx from pi/6 to pi/2
so (3/2)x-2cos(x) -1/4 sin(x) from pi/6 to pi/2
comes out to 2pi/4 + (7√3)/8
then I have the other segment
a= 2×1/2 ∫ (3sin(x))^2 dx from 0 to pi/6
(9/2)x-(9/2)sin(2x)
for which I get 3pi/4 - (9√3)/8
which totals up to 7pi/4 -(2√3)/8
and according to my professor's key the answer is pi
needless to say I am lost.