SUMMARY
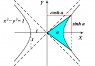
The discussion focuses on calculating the area sector of a unit hyperbola defined by the equation x² - y² = 1 using the inverse hyperbolic functions arcsinh and arcosh. The user seeks a numerical example and graphical representation to illustrate how these functions can compute the area. Key formulas include arcsinh(x) = ln(x + √(x² + 1)) and the relationships between area, sinh(a), and cosh(a) as they relate to points on the hyperbola. The discussion references a Wikipedia page for definitions and further explanations.
PREREQUISITES
- Understanding of hyperbolic functions, specifically sinh and cosh.
- Familiarity with inverse hyperbolic functions, particularly arcsinh and arcosh.
- Basic knowledge of calculus, particularly area under curves.
- Ability to interpret and create graphs of mathematical functions.
NEXT STEPS
- Study the derivation and properties of inverse hyperbolic functions.
- Learn how to compute areas under hyperbolic curves using integration techniques.
- Explore graphical representations of hyperbolic functions and their inverses.
- Investigate applications of hyperbolic functions in real-world scenarios, such as physics and engineering.
USEFUL FOR
Mathematicians, physics students, and anyone interested in advanced calculus and hyperbolic functions will benefit from this discussion, particularly those looking to deepen their understanding of area calculations involving hyperbolas.