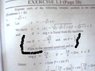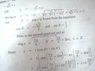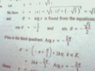kayanian
- 2
- 0
-1-(under root)3 i
here we find that
r=2(hypotenuse)
a=-1(base)
b=-(under root)3
when i take sin theat= p/h=-(under root)3 / 2
theat from sin is -60
when i take cos theta = b/h =-1 / 2
which gives 120
now one is -60 and other is 120, which is the angel , i have to follow and what do i add it to?
here we find that
r=2(hypotenuse)
a=-1(base)
b=-(under root)3
when i take sin theat= p/h=-(under root)3 / 2
theat from sin is -60
when i take cos theta = b/h =-1 / 2
which gives 120
now one is -60 and other is 120, which is the angel , i have to follow and what do i add it to?
Attachments
Last edited: