aheight
- 318
- 108
The graph posted in #15 is misleading at it's endpoints outside of ##(e^{-e},e^{1/e})##: The command used to plot it was:
[CODE title="Mathematica"]Nest[Sin[theta]^# &, 1, 800]
[/CODE]
So that's just iterating the tetration of ##\sin(t)## 800 times. But when ##\sin(t)<e^{1/e}##, the tetration is no longer single valued but rather enters a 2-cycle oscillation and selecting the even number of iterations was just selecting the higher value. Consider the output:
[CODE title="Mathematica"]In[59]:= Nest[Sin[0.02]^# &, 1, 500]
Nest[Sin[0.02]^# &, 1, 501]
Out[59]= 0.884202
Out[60]= 0.0314587[/CODE]
This is what a plot of ##\sin(t)\uparrow\uparrow \infty ## really looks like on ##(0,\pi)##:
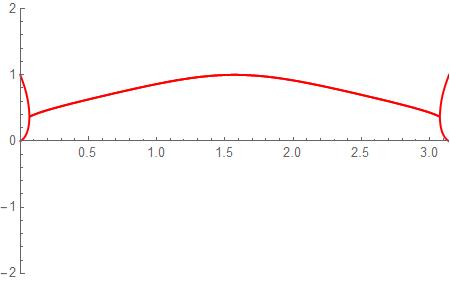
[CODE title="Mathematica"]Nest[Sin[theta]^# &, 1, 800]
[/CODE]
So that's just iterating the tetration of ##\sin(t)## 800 times. But when ##\sin(t)<e^{1/e}##, the tetration is no longer single valued but rather enters a 2-cycle oscillation and selecting the even number of iterations was just selecting the higher value. Consider the output:
[CODE title="Mathematica"]In[59]:= Nest[Sin[0.02]^# &, 1, 500]
Nest[Sin[0.02]^# &, 1, 501]
Out[59]= 0.884202
Out[60]= 0.0314587[/CODE]
This is what a plot of ##\sin(t)\uparrow\uparrow \infty ## really looks like on ##(0,\pi)##:
Last edited: