ART algorithm - Image Reconstruction

In summary, the ART (Algebraic Reconstruction Technique) algorithm is a mathematical method used for reconstructing images from a set of projection data. It works by iteratively improving an initial estimate of the image until it fits the available projection data. Its advantages include its ability to handle incomplete or noisy data, relatively fast computation time, and production of high-quality images with minimal artifacts. However, it can be computationally intensive and requires a good initial estimate. The ART algorithm is commonly used in medical imaging, particularly in CT imaging, and also in other imaging techniques such as PET and SPECT.
  • #1
nao113
68
13
Homework Statement
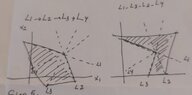
Some iterative algorithms, for example, the ART algorithm, update the image very frequently. For those algorithms, the processing order of the data subsets is important. In this problem, we use the ART algorithm to graphically solve a system of linear equations {𝐿1, 𝐿2, 𝐿3, 𝐿4} with two variables as shown in the figure below. The initial estimated solution is 𝑋0. Solve the system with two different orders: (a) 𝐿1 → 𝐿2 → 𝐿3 → 𝐿4 and (b) 𝐿1 → 𝐿3 → 𝐿2 → 𝐿4 , respectively. Compare their performance in terms of convergence rate.
Relevant Equations
In the picture below
Screen Shot 2022-06-09 at 15.50.49.png

My answer:
The ART algorithm is a row-action algorithm.
I tried to draw it, but I am not sure whether it will answer the question
 

Attachments

  • WhatsApp Image 2022-06-10 at 2.15.40 PM.jpeg
    WhatsApp Image 2022-06-10 at 2.15.40 PM.jpeg
    20.1 KB · Views: 109
Physics news on Phys.org
  • #2

FAQ: ART algorithm - Image Reconstruction

What is ART algorithm and how does it work?

The Algebraic Reconstruction Technique (ART) algorithm is a computational method used in image reconstruction. It works by iteratively updating the image estimate based on the difference between the measured data and the estimated data. It uses a system of linear equations to solve for the image pixels and converges to a solution that minimizes the error between the measured and estimated data.

What are the advantages of using ART algorithm for image reconstruction?

ART algorithm has several advantages, including its ability to handle incomplete and noisy data, its fast convergence rate, and its ability to reconstruct images with high spatial resolution. It also allows for the incorporation of prior knowledge about the image, which can improve the quality of the reconstruction.

What are the limitations of ART algorithm?

One of the main limitations of ART algorithm is its high computational cost, as it requires a large number of iterations to converge to a solution. It also assumes that the image is composed of a small number of distinct objects, which may not always be the case. Additionally, ART algorithm may struggle with images that have high levels of noise or artifacts.

How is ART algorithm different from other image reconstruction techniques?

Unlike other techniques that use analytical methods or statistical models, ART algorithm uses a purely algebraic approach to reconstruct images. This allows it to handle a wider range of data types and to incorporate prior knowledge about the image. Additionally, ART algorithm is an iterative method, which means it can continuously improve the image estimate until convergence is reached.

What are some applications of ART algorithm in scientific research?

ART algorithm has been widely used in various fields of scientific research, including medical imaging, astronomy, and materials science. It has been used to reconstruct 3D images of biological tissues, to study the structure of galaxies and other celestial objects, and to analyze the microstructure of materials. It has also been used in tomography and other imaging techniques to improve image quality and reduce artifacts.

Similar threads

Comp Sci I need a solved numerical example on genetic algorithm for 1 iteration
Replies
11
Views
1K
Comp Sci Confused about DFS algorithm in action (not an issue with the pseudocode)
Replies
16
Views
3K
Time Taken by this Algorithm in Terms of m, p, t_add, t_s and t_w
Replies
1
Views
1K
Comp Sci For which of the following purposes is the Banker’s algorithm used?
Replies
1
Views
2K
Comp Sci What I am supposed to write in this question about fuzzy logic?
Replies
9
Views
1K
Comp Sci Find a Best-Case Example of QuickSort
Replies
8
Views
2K
Algorithm for computing the depths of all the nodes of tree
Replies
1
Views
2K
Comp Sci When is a problem said to be decidable or undecidable?
Replies
1
Views
1K
Engineering Black-box design to create sawtooth waveform
2
Replies
49
Views
4K
Comp Sci Complexity for generating strings of length k from CNF grammar
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top