I Autocorellation of a stochastic process

[PHstud]

Hello ! I am trying an exercice to get a better grip of what is the autocorellation meaning.
I know the mathematical formula, but let's consider a case.

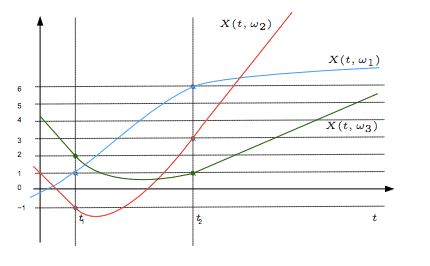
If in the case above, the probabilty of the red curve to happen (so w2) is Pr, the blue one Pb and the green on Pg, what would be the result of the autocorellation ?
Would it be something like the sum of the value X(t1,w1)*X(t2,w2)*Pb*Pr + X(t1,w1)*X(t3,w3)*Pb*Pg + ... ?

Thank you for helping me !

 

[FactChecker]

Do you mean to say cross-correlation rather than autocorrelation? Autocorrelation only refers to a single time series and the correlation of that time series with a delay of itself. Your equations seem to be for cross-correlations. But even then, a cross-correlation is between two time series, not three.

You need to tell us what math formula you were given, that you say you know.

 

[PHstud]

I do mean autocorellation.
These 3 curves belong to a stochastic signal, and each realisation has a probability to happen and result in one of those trajectories

 

[FactChecker]

Since the result is one of those three time series, you have three autocorrelation functions, one for each time series. Each of the three would be the normal autocorrelation. If you want a function that combines all three, you should first carefully define what you want the function to represent. I can't think of anything along the lines of autocorrelation that would apply.

 

[PHstud]

But if we consider each serie individually, don't we lose the 'stochastic' behaviour of the process ?

 

[FactChecker]

Only the random selection of which trajectory to follow involves more than one path. That selection should not be involved in an autocorrelation calculation. I would not call the initial selection of the trajectory part of a stochastic process. I would treat it separately as a simple probability because its nature is completely different from the remainder of the problem.

 

[Stephen Tashi]

You should define the stochastic process clearly:

$X(t)$ is a random variable given by the distribution:

$P(X(t) = f_r(t)) = r$

$P(X(t) = f_g(t)) = g$

$P(X(t) = f_b(t) = b$

Since you imply the trajectory of the process has only 3 possibilities, we can think of realizing it as making one random draw to determine the value of $X(0)$. If the draw selects $f_r$ then $X(t) = f_r(t) = f_r(s)$ etc. In other words we don't make a random draw at $X(s)$ and make a different random draw at $X(t)$.
( Saying "the process has only 3 possible trajectories" is different that saying "at each time t, we select the value of the process from one of 3 possible functions". )
The autocorrelation function is defined by

$R(s,t) = \frac { E ( (X(s) - \overline{X(s)} )(X(t) - \overline{X(t)} )}{\sigma_s \sigma_t}$
Start by finding the constants $\overline{X(s)}, \sigma_s, \overline{X(t)}, \sigma_t$.
For example, $\overline{X(s)} = r f_r(s) + g f_g(s) + b f_b(s)$

$\sigma_s = \sqrt{ E(X(s)^2) - \overline{X(s)}^2}$

$= \sqrt{ r f_r(s)^2 + g f_g(s)^2 + b f_b(s)^2 - (\overline{X(s)})^2 }$
Once you find those constants, the expectation symbol "$E$" implies you compute the expected value of the function $g(s,t) = \frac { (X(s) - \overline{X(s)} )(X(t) - \overline{X(t)}}{\sigma_s \sigma_t}$
Since we only make one random draw, the function $g(r,s)$ has 3 possible values

$P ( g(s,t) = \frac{( f_r(s) - \overline{X(s)})(f_r(t) - \overline{X(t)})}{ \sigma_s \sigma_t}) = r$
$P ( g(s,t) = \frac{( f_g(s) - \overline{X(s)})(f_g(t) - \overline{X(t)})}{ \sigma_s \sigma_t}) = g$
$P ( g(s,t) = \frac{( f_b(s) - \overline{X(s)})(f_b(t) - \overline{X(t)})}{ \sigma_s \sigma_t}) = b$

Maybe there is some theorem that can be used to avoid all the algebra. (That's not a hint, because, off hand, I don't remember one.)