artis
- 1,479
- 976
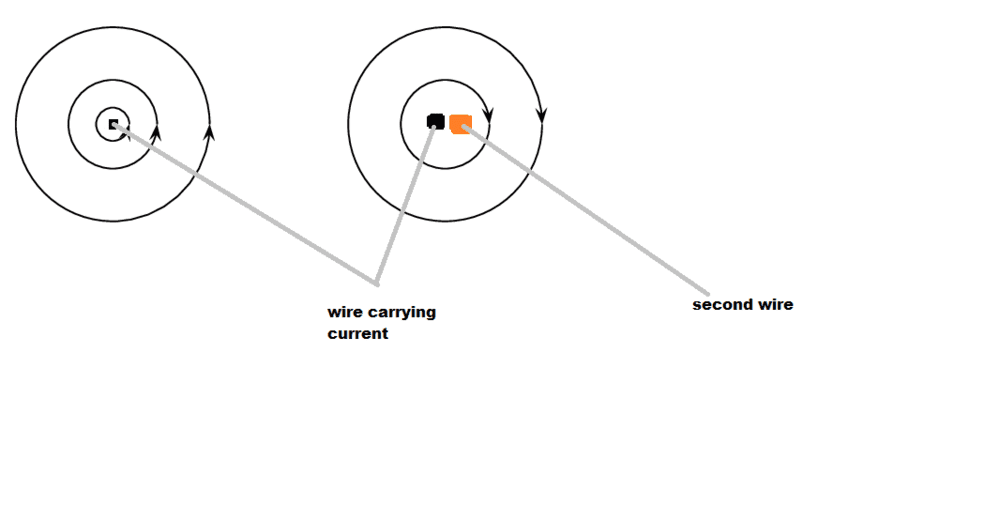
A quick description. A single straight wire and a second straight wire, both wires are electrically as well as physically separated, the physical separation distance assume is very small in order for the B field experienced by the second wire to be sufficiently strong.
In all cases one of the wires is connected to a power supply and has current in it the other wire is connected to a test meter for current and voltage.
Here is what I want to understand. When current flows through a wire there is a B field around the wire commonly shown as an arrow forming a loop around the wire, what happens when I place a conducting object at any point next to the wire , does in theory the B field experienced by that conducting object (a piece of conducting foil for example) is cutting the object at 90 degrees and can be said to be perpendicular to it?
I've attached a picture with a drawing which is made such that (you) the observer is looking from the top of the wire end.
So if a DC current passes through the first wire a static B field is set around it and this B field penetrates as well as loops around the second adjacent wire (shown in orange) , I wonder what happens with AC, especially high frequency all the way up to RF?
I would expect that as the frequency increases the field penetration depth decreases , what happens now? Can we still say the B field is cutting the second wire/conductor perpendicularly or is it now looping entirely around it due to induced surface eddy currents in the second wire/conductor?
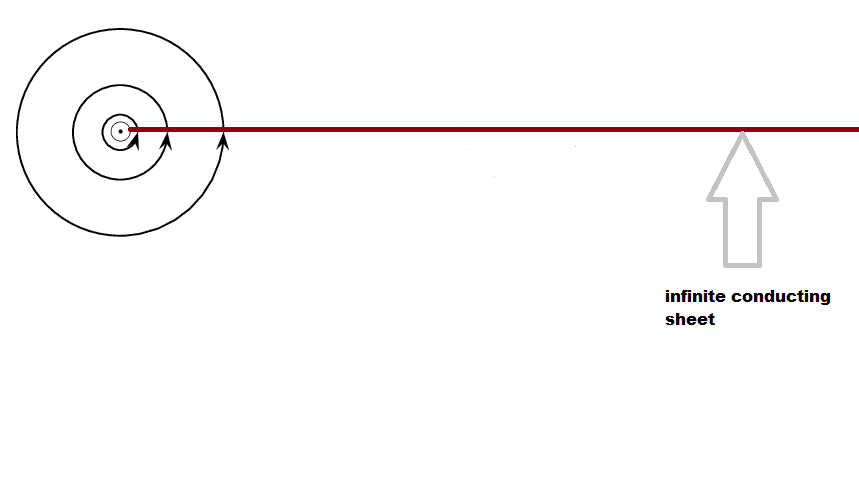
And lastly, what happens when there is the same current carrying wire but now the adjacent wire is an infinite conducting sheet extending from the side of the current carrying wire away till infinity, in DC case the field would eventually go through the sheet but in AC case?
How would the AC current be affected in the wire if the wire's B field was "blocked" for the entire length of the wire?
thanks.
In all cases one of the wires is connected to a power supply and has current in it the other wire is connected to a test meter for current and voltage.
Here is what I want to understand. When current flows through a wire there is a B field around the wire commonly shown as an arrow forming a loop around the wire, what happens when I place a conducting object at any point next to the wire , does in theory the B field experienced by that conducting object (a piece of conducting foil for example) is cutting the object at 90 degrees and can be said to be perpendicular to it?
I've attached a picture with a drawing which is made such that (you) the observer is looking from the top of the wire end.
So if a DC current passes through the first wire a static B field is set around it and this B field penetrates as well as loops around the second adjacent wire (shown in orange) , I wonder what happens with AC, especially high frequency all the way up to RF?
I would expect that as the frequency increases the field penetration depth decreases , what happens now? Can we still say the B field is cutting the second wire/conductor perpendicularly or is it now looping entirely around it due to induced surface eddy currents in the second wire/conductor?
And lastly, what happens when there is the same current carrying wire but now the adjacent wire is an infinite conducting sheet extending from the side of the current carrying wire away till infinity, in DC case the field would eventually go through the sheet but in AC case?
How would the AC current be affected in the wire if the wire's B field was "blocked" for the entire length of the wire?
thanks.