Back of the envelope estimate, energy flow in a box of plasma

[Spinnor]

Say we look at a spherical region of the sun where energy is mainly transported by radiation. Say this happens between some particular radius R and R + dr. Let the temperature at R be giving by T(r). At this particular radius let the gravitational acceleration be a reasonably well know function of r, g_sun(r). Assume the temperatures are so high that nearly all matter in this region is ionized. Assume the density of matter at and near R is given by another good function of r, rho_sun(r).

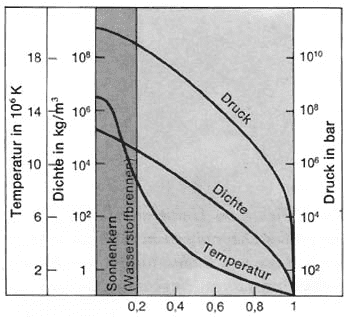
Given the information above show there is, or is not, also a function of all the factors above (might be missing some) that gives the electric polarization in the sun at R given by P(T(R), g_sun(R), rho_sun(R)), however small its value might be at R.

How should I break down the above problem to come up with a back of the envelope answer. The Klein-Nishina formula tells us that even if small, the average outward radial movement of light in the interior of the sun should give a bit of an outward "kick" to charged matter? Because the interaction cross-section of light and matter goes as 1/m^2, the electrons get "kicked" by light more then protons? This is where I get stuck analyzing this problem.

Thanks for any help suggestions moving this problem forward.

 

[WernerQH]

At the surface of the sun the flux of radiation is $L / 4\pi R^2 = 6.28 × 10^{7} {\rm W m^{-2}}$. Dividing by the speed of light I get a radiation pressure of $0.21 {\rm N m^{-2}}$. Multiply that by the Thomson(!) cross section to get $1.4 × 10^{-29} \rm N$ for the force on an electron. Or $8.7 × 10^{-11} \rm eV/m$. In the interior of the sun this value would be even smaller. It seems you need only an extremely small electric field of less than a nanovolt per meter to balance the radiation pressure.

the electric polarization in the sun [...], however small its value might be

Is this the quantity you had in mind? It is small indeed, unless I have miscalculated!