- #1
anon11
- 9
- 1
Can someone please help me out with this tough problem?
1. Homework Statement
A ball rolls on a turntable without slipping describe the balls motion in terms of (x,y) for a function of time. (The turntable spins at a constant rate)
(This all the information that the professor gave us.)
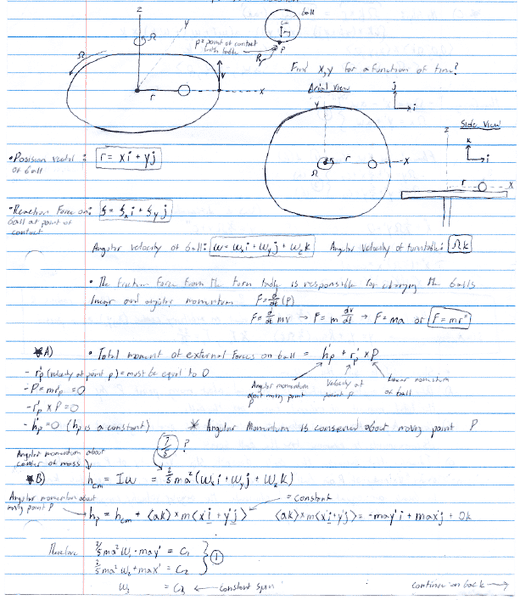

My professor said the answer has 7/5 in it somewhere. Can someones please help? I'm really confused about this problem.Here are some sources that helped me get my answer:
http://www.warrenweckesser.net/pubs/AJP_BallRolling.pdf
http://www.tyoma.com/plain/science/papers/14/ball.pdf
https://www.physics.harvard.edu/uploads/files/undergrad/probweek/sol21.pdf[/B]
1. Homework Statement
A ball rolls on a turntable without slipping describe the balls motion in terms of (x,y) for a function of time. (The turntable spins at a constant rate)
(This all the information that the professor gave us.)
The Attempt at a Solution
My professor said the answer has 7/5 in it somewhere. Can someones please help? I'm really confused about this problem.Here are some sources that helped me get my answer:
http://www.warrenweckesser.net/pubs/AJP_BallRolling.pdf
http://www.tyoma.com/plain/science/papers/14/ball.pdf
https://www.physics.harvard.edu/uploads/files/undergrad/probweek/sol21.pdf[/B]