- #1
catsarebad
- 72
- 0
Could someone explain to me how the author goes from 2nd to 3rd step
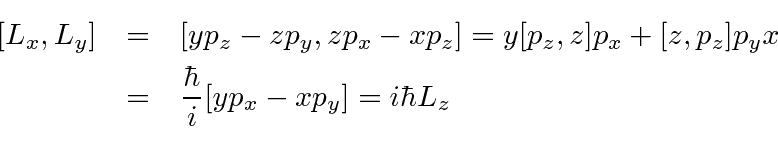
I think the intermediate step between 2 and 3 is basically to split up the commutator as
[y p_z, z p_x] - [y p_z,x p_z] - [z p_y,z p_x] + [z p_y, x p_z]
2nd term = 0
3rd term = 0
so leftover is
[L_x, L_y] = [y p_z, z p_x] + [z p_y, x p_z]
but how does this turn into what he has on 3rd step?
I think the intermediate step between 2 and 3 is basically to split up the commutator as
[y p_z, z p_x] - [y p_z,x p_z] - [z p_y,z p_x] + [z p_y, x p_z]
2nd term = 0
3rd term = 0
so leftover is
[L_x, L_y] = [y p_z, z p_x] + [z p_y, x p_z]
but how does this turn into what he has on 3rd step?