hubbard97
- 1
- 1
- Homework Statement
- A proton beam of kinetic energy 20 MeV enters a dipole magnet 2 m in length.
How strong must the field be to deflect the beam by 10 degrees?
- Relevant Equations
- F = qvB
I haven't taken a physics courses in some time and I'm having trouble getting started with this textbook question. I know that there will be relativistic effects present, but I can deal with that. The problem is how I can approach the problem. I initially thought of a geometric way to set up the problem where I simply assume magnetic field will exert a force uniformly:
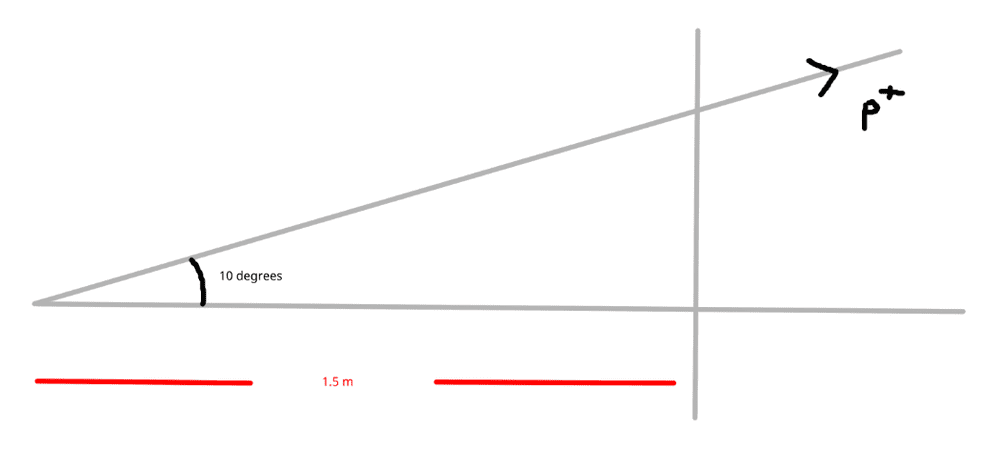
But I'm not sure if this will work out since the magnetic field will technically induce a circular motion. Any guidance would be greatly appreciated!
But I'm not sure if this will work out since the magnetic field will technically induce a circular motion. Any guidance would be greatly appreciated!