Bevington and uncertainty of a weighted mean

[pkennedy]

I'm trying to decide on a method for calculating a weighted mean for my data.

In Bevington's Data Reduction and Error Analysis for the Physical Sciences 2nd Ed. Equation 4.19, the variance of the weighted mean is:

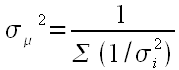
However, Bevington also suggests the use of Equation 4.22 substituted into 4.23 to calculate the variance of the weighted mean:

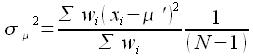
These two formula are not equivalent (even if weight is defined as the square of the inverse standard deviation).

To muddy the waters even further, a coworker has suggested the following variance calculation:

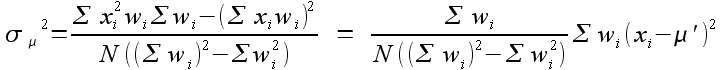
Could someone explain why these formulae are different when they are all used to calculate the standard deviation of the weighted mean? Do they serve different purposes?

 

[pkennedy]

Further information:

Equation 4.19 was derived by applying the error propagation equation:

to the equation for the weighted mean:

https://www.physicsforums.com/attachment.php?attachmentid=30258&d=1291222596.

On the other hand, the substitution of Equation 4.22 into Equation 4.23 appears very much like the definition of standard deviation (tweaked for weighted values).

Shouldn't the uncertainty on the weighted mean calculated in Equation 4.19 be identical to the uncertainty calculated by the substitution of Equation 4.22 into 4.23?

 

[ych22]

I can only provide a lay explanation about which to use, not the mathematical derivation sorry.

The first equation arises when each observation comes from a different probability distribution with known variance \sigmai and we assign weights to the observations based on their known variance such that w_i=1/\sigmai^2. Therefore there is no more w_i term in the variance formula.


The second equation arises when you do not know the variances of the observations before hand obviously. And actually, without the known variances, you are merely computing an estimate of the variance of the mean, not computing the variance of the mean. It would be more appropriate to write \widehat{\mu}²= ... instead.

The tangible difference between them (if you do not understand estimation theory and are just interested in this for your work...because I do not really understand or can explain it well either) is that the first formula can be calculated before any data is calculated as we are working with presumably known information, but the second formula can only be calculated with the data and their mean.

The third equation...well... I cannot really verify it at the moment but I think N-1 should be used instead of N to correct for biasness. The question is, is the second formula or the third formula a better estimator for variance of mean? I suspect the additional terms are included to correct biasness.

Edit: damn latex I can't figure out the problem with the notation

 

[pkennedy]

Thank you very much for your reply.

The second equation arises when you do not know the variances of the observations before hand obviously. And actually, without the known variances, you are merely computing an estimate of the variance of the mean, not computing the variance of the mean. It would be more appropriate to write LaTeX Code: \\widehat{\\mu} 2= ... instead.

So the difference between the first equation (4.19) and the second (4.22 into 4.23) is that the first equation (given precisely known variances) will produce the exact variance of the weighted mean but the second equation will produce an estimate of the variance of the weighted mean?

[Edit]:
This raises a practical question: if the weights used to calculate the weighted mean are equal to the inverse square of *estimates* of the variances (obtained by the typical unweighted variance calculations on measured data), is the first or second equation more appropriate?

 

[ych22]

The first one then. But usually when we substitute sample variance into an equation requiring known population variance directly, some correction has to be done depending on the distribution of the data.

For example, the t-test and z-test are both applied on a test on the sample mean, depending on whether the population variance is assumed to be known or unknown.

 

[pkennedy]

I vaguely recall using those tests before but not for the purpose of correcting data. I'll need to look for a resource to explain how these corrections should be done (any suggestions?).

Thanks again.