Block held by a rope on an incline

[trolling]

Homework Statement

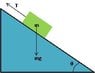
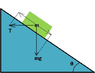
A block with mass m1 = 9.4 kg is on an incline with an angle θ = 31.0° with respect to the horizontal. There is also a massless rope that pulls horizontally to prevent the block from moving. What is the tension in the rope?

Homework Equations

Fg = m*g
Fg,x = m*g*sin 31 = Tx (?)
Fg,y = m*g*cos 31 = Fn
Ff = u*Fg,y

The Attempt at a Solution

Fg = 9.4kg*9.8m/s^2 = 92.12N
Fg,x = Tx(?) = 92.12N * cos 31 = 84.156N
Fg,y = Fn = 92.12N * sin 31 = 37.469N
Ff = u * Fn

I had a value for the coefficient of static friction, but that was for a system with a spring (.292), so I don't think that'll work here. I also have one for kinetic friction (.212), but that might not apply here. I'm a little unsure in finding the tension in the x-direction, since I'm pretty sure if I can find that, I can find the overall tension using Tx/cos31. But after that, I'm stuck.

 

[Saitama]

Start by making a free body diagram. If you aren't given any information about the coefficient of friction in the question, why to deal with it? ;)

The body is in rest. So the tension must be balanced by one of the components of the weight.

 

[trolling]

Start by making a free body diagram. If you aren't given any information about the coefficient of friction in the question, why to deal with it? ;)

The body is in rest. So the tension must be balanced by one of the components of the weight.

Ok, I have a FBD set up, but since this site won't let me post it, I can't show it. Looking at your last statement, I'm guessing that the x-component of the weight (37.469N) MIGHT be equal to the x-component of the tension. I then used that component to divide by cos 31° to get the overall tension, which I got to be 43.713N; however, my solutions box won't accept that as an answer.

 

[Saitama]

(see attachment)
The tension on the block acts as shown in the attachment, not in the x-direction. As i already said, a component of weight balances tension. Your job is to find that component.

 

[ehild]

Trolling, could you please copy the full text of the problem? The static friction has to be taken into account if it was given for the same slope and block. Also, is it really said that the string pulls horizontally to prevent the block from sliding? That is rather impossible. The block can be pulled by a string along the slope, as in Pranav-Arora's picture.
When you set up a coordinate system, indicate the direction of the axes. Here, the x-axis is parallel to the slope, the y-axis is perpendicular to it.

You can upload pictures up to 300 KB. Make a jpg file of your drawing, click on "Go Advanced" then "Manage Attachments". Or you can upload files to http://imageshack.us/ and give the URL.

ehild

 

[Saitama]

You can upload pictures up to 300 KB. Make a jpg file of your drawing, click on "Go Advanced" then "Manage Attachments". Or you can upload files to http://imageshack.us/ and give the URL.

If i remember correctly, he cannot post links until he has a post count of 10.

 

[CWatters]

(see attachment)
The tension on the block acts as shown in the attachment, not in the x-direction. As i already said, a component of weight balances tension. Your job is to find that component.

Err According to the OP the problem says the rope is horizontal so the tension in it does act in the x-direction.

 

[CWatters]

Trolling, could you please copy the full text of the problem? The static friction has to be taken into account if it was given for the same slope and block. Also, is it really said that the string pulls horizontally to prevent the block from sliding? That is rather impossible.

It's NOT impossible. If the string acts to the left it will stop the block sliding down the slope.

 

[CWatters]

If I've understood the problem it looks like this. There is a component of weight acting down the slope that must be balanced by the component of T acting up the slope.

If this is a multipart question and the first part gives you info on friction then you need to factor that in as well. Otherwise treat as frictionless.

 

[trolling]

(see attachment)
The tension on the block acts as shown in the attachment, not in the x-direction. As i already said, a component of weight balances tension. Your job is to find that component.

Actually, the trick here is that the rope is actually perpindicular to the force of gravity.

 

[ehild]

It's NOT impossible. If the string acts to the left it will stop the block sliding down the slope.

I just wonder how it can be realized. Imagine you tilt a table and put a book on it, you attach a string to the book, - how do you manage to pull the string horizontally? Drilling a hole through the table?

ehild

 

[ehild]

Actually, the trick here is that the rope is actually perpendicular to the force of gravity.

The weight of the block has a component parallel to the slope and an other component perpendicular to it. The horizontal force of tension also can be resolved into parallel and perpendicular components. The normal force balances the sum of both perpendicular components, those of the weight and the tension. Friction acts along the slope, upward.

ehild