Homework Help Overview
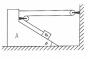
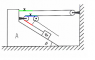
The discussion revolves around the relationship between the acceleration of a block on a movable wedge and the acceleration of the wedge itself, within the context of a pulley system. Participants are examining the dynamics involved when the wedge moves and how it affects the block's motion.
Discussion Character
- Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants are exploring the relationship between the accelerations of the block and the wedge, with some attempting to derive equations based on the geometry of the system. Questions are raised regarding the assumptions made about the movement of the string and the implications of the wedge's motion on the block's acceleration.
Discussion Status
There is an ongoing examination of the reasoning behind the relationships proposed. Some participants have offered alternative perspectives on the string's behavior and the resulting motion of the block. Multiple interpretations of the problem are being explored, and participants are questioning the validity of initial assumptions without reaching a consensus.
Contextual Notes
Participants are discussing the implications of the inextensibility of the string and the geometric relationships involved in the system. There are references to specific angles and distances that may affect the calculations, but no definitive conclusions have been drawn.