- #1
arpon
- 235
- 16
If both the plates of a capacitor are connected to positve voltage, (but has a potential differnce between them) will the capacitor be charged? And how?
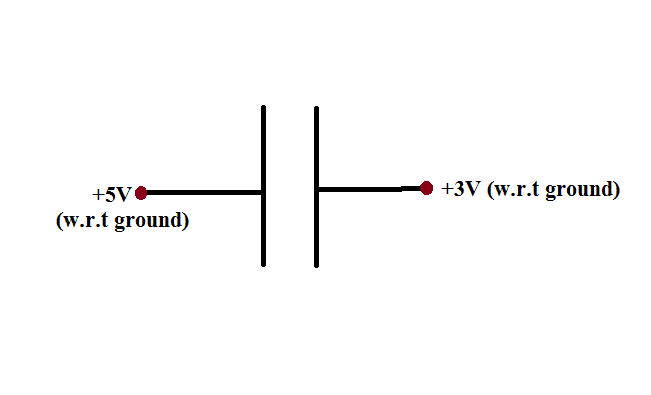
Actually, by 'ground', I mean something which is electrically neutral. Both of the plates are connected to some conductor which has lack of electrons (and so they are electrically positive). But the voltages of the plates are not the same.Bystander said:And what potential is this particular ground at with respect to another ground? Does the ground potential matter?
Why not? It's [itex](+5V) - (+3V) = 2V[/itex]Drakkith said:Well, if one plate is charged to +5v and the other to +3v, is there a potential difference between them?
In a capacitor, one of the plates is charged positive and the other negative and they are equal in quantity. But in this case, both the plates lack electron. So how can it provide negative charge or, electron?Drakkith said:Okay. So if the potential between the plates is 2 volts, do you think the capacitor is "charged"? Why or why not?
Drakkith said:Both plates lack a very, very small number of electrons. Over 99.999% of the electrons are still on the plates. The plate charged to +5v simply has a few more electrons missing. A few missing electrons adds up to a large amount of charge.
How can the plate have negative charge, but positive electric potential?Drakkith said:Not at all. The plate will lose electrons until it reaches +3 volts. It will then stop losing them and remain at +3v.
arpon said:How can the plate have negative charge, but positive electric potential?
So, you are saying, both the plates will have positive charges?Drakkith said:It doesn't have a "negative charge", it has -2 volts of potential relative to ground compared to the +5v plate. Remember that electric potential is measured between two points. Measuring the voltage between the ground and each plate gives you +3v and +5v, but measuring from one plate to the other gives you either +2v or -2v. In other words, if you measure the voltage between the plates with a volt meter, you'll get either +2v or -2v depending on how you place the leads. Switching them around will cause current to flow the other way through the voltmeter and it will read the voltage a being the opposite sign.
arpon said:So, you are saying, both the plates will have positive charges?
anorlunda said:arpon,
Absolute potentials don't matter, only relative potentials. You could label both plates as +5 +3 or +1005 +1003 or -1005 -1003, and the result is the same.
Zero volts, is an arbitrary choice. We normally choose "ground" as zero volts becasuse it is natural and convenient. But other choices for zero work just as well.
An "uncharged object" has the same number of electrons as protons. But even an uncharged object can have a plus or minus potential difference between it and some other object.
Think relative, not absolute voltage. Balls roll down a ramp the same if the ramp is at the top of a mountain or at the bottom of a valley, as long as one end of the ramp is at a height higher relative to the other end.
Drakkith said:Relative to ground, yes.
arpon said:In the typical situation (which is most commonly described in textbooks), one of the plate is charged [itex]+Q[/itex] and the other [itex]-Q[/itex]; If the potential difference is [itex]V[/itex], then the capacitance is defined as [itex]C = \frac{Q}{V}[/itex].
Then, what it would be in this case as I mentioned in post #1. My question is in the point that Drakkith said both the charges are positive.
A capacitor is an electrical component that stores energy in an electric field. It is made up of two conductive plates separated by an insulating material, known as a dielectric.
The plates of a capacitor can be connected to positive voltage by attaching one plate to the positive terminal of a voltage source, such as a battery, and the other plate to the negative terminal. This creates an electric field between the plates and stores energy in the capacitor.
When both plates of a capacitor are connected to positive voltage, the capacitor becomes charged. Electrons from the negative plate are attracted to the positive plate, creating an electric field between the plates.
Yes, a capacitor can be connected to any type of voltage, as long as the voltage is within the capacitor's voltage rating. It is important to check the capacitor's rating before connecting it to a voltage source to avoid damaging the capacitor.
A capacitor connected to positive voltage can be used in various electronic devices, such as power supplies, audio equipment, and electronic circuits. It is commonly used to store energy, filter signals, and regulate voltage in a circuit.