Boundary conditions for convective heat and mass transfer + wall Temperature

[maistral]

I am operating via finite differences.

Say for example, I have this pipe that contains a fluid. I have the boundary condition at x = x₁:

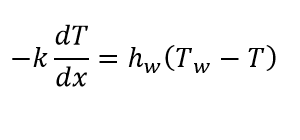
k is the effective thermal conductivity of the fluid, T is the temperature of the fluid at any point x, h_w is the wall heat transfer coefficient, and T_w is the temperature at the wall.

I know how to 'plug in' such boundary conditions in finite difference formulations. My question is which value of T do I use? Is it T at x = x₁? But isn't that T_w already, since x₁ is the wall?

I keep on seeing that T here is supposed to be the bulk temperature. The problem is since I'm doing this by finite difference, the temperature of the fluid is not constant along the spatial dimension. In this case, which point to use exactly? Is it the point at the fluid beside the wall point?

Or is it that at the 'wall point', there are 'two operating temperatures' - the 'wall temperature' and the 'bulk fluid temperature' at the wall?

Any help is appreciated. Thank you!

 

[maistral]

EDITED; Additional info:

The first equation written below is the boundary condition I lifted directly from a book. If I express the boundary condition in terms of finite differences, I write it as the second equation, am I correct?

But if I do write it as the second equation, isn't T(r) just equal to T_w(r), since this boundary condition is applied at the wall? Or am I missing something here?

Or T_w(r) is indeed, the temperature at the wall (r = d/2)? If then, what is T in the RHS of the equation, and at which value of r do I evaluate it? Certainly it should not be r = d/2 since it would just cancel out?

 

[maistral]

This graphic should sum up my rather, annoying problem that makes me look like someone who wants to constipate. Please help.

 

[Chestermiller]

You are aware that Tb is supposed to be the exterior imposed temperature of the surrounding medium, outside the thermal boundary layer at the wall. It has nothing to do with the wall temperature. I assume you are solving a transient problem, correct? Your boundary condition equation should read: $$-\lambda\frac{(T_5-T_3)}{2\Delta x}=h_w(T_b-T_4)$$This should be combined with your transient differential equation at point 4 to eliminate $T_5$.

 

[maistral]

Allow me to reinforce my understanding.

In your equation, this means T_b is the bulk temperature at the right side (outside) of the wall, yes?

 

[Chestermiller]

Allow me to reinforce my understanding.

In your equation, this means T_b is the bulk temperature at the right side (outside) of the wall, yes?

Yes. Of course, T5 is a fictitious temperature that gets eliminated by combining with the discretized transient energy balance equation at point 4.