- #1
DumpmeAdrenaline
- 78
- 2
- Homework Statement
- Consider a tubular reactor with a non-porous catalyst coated on the wall. A liquid solution
containing reactant A flows through the tube in laminar flow with an inlet concentration, CA0 . The reaction:
A⇌B
occurs homogeneously via a first order reaction and heterogeneously via a Langmuir-Hinshelwood mechanism:
A+S⇌A-S
A-S⇌B-S
B-S⇌B+S
where S represents a surface site and the surface reaction is rate controlling. The reactor is heated electrically which gives a constant heating flux over the entire reactor. Derive the relevant PDE which describe the reactor (2-D model) and give the necessary boundary conditions. Do not solve the equation.
- Relevant Equations
- 2D Heterogeneous Model
My attempt:
Species fluid and solid phase balances for a tubular reactor in which there is a homogeneous first order reaction and a heterogeneous reaction on the external surface of non-porous catalyst coated along the reactor wall.
Mole balance equation for the fluid phase
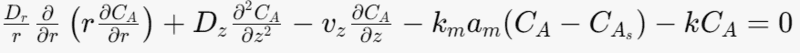
The heterogeneous reaction is represent by mass transfer to the solid phase.
Where Dr-radial diffusion coefficient
Dz- Axial diffusion coefficient [m^2/s]
vz- superficial fluid velocity [m/s]
km- mass transfer coefficient [m/s]
am- particle surface area per unit bed volume [m^-1]
k-rate constant [s^-1]
Solid Mole balance equation for the solid phase
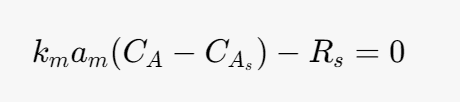
Rs- heterogeneous rate of reaction (LHHW)
1)A+S⇌A-S (chemisorption of A)
2)A-S⇌B-S (Surface reaction)
3) B-S⇌B+S (Desorption of B)
2) is the rate determining reaction and 1) and 3) are assumed to be in equilibrium.
There is a single type of site and there is competitive adsorption between A and B.
The rate of adsorption is given by
At equilibrium the net rate of adsorption and desorption are 0. Therefore the surface coverage by A and B are given by.
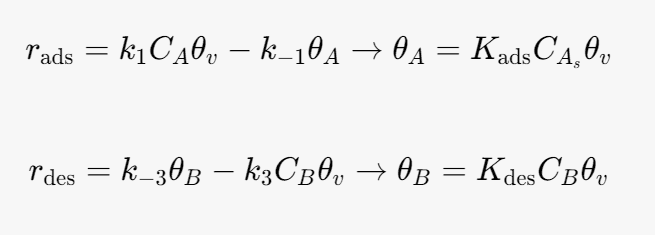
where θv is the fraction of vacant sites.
Site balance:
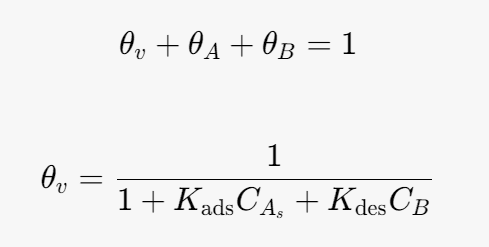
Substitute into the rate determining step (rate equation):
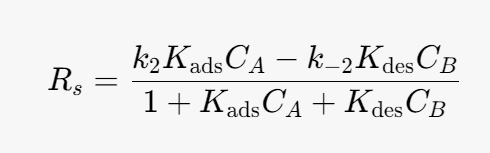
We can simplify the above equation using the equilibrium constant for the heterogeneous reaction. At equilibrium the surface reaction is equal to 0.
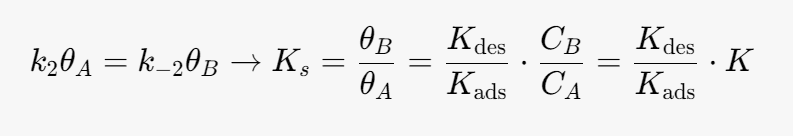
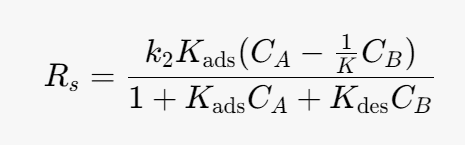
Kads- [m^3/mol]
Kdes- [m^3/mol]
k2 -[mol/(m^3*s)]
Energy Balance for the fluid phase:
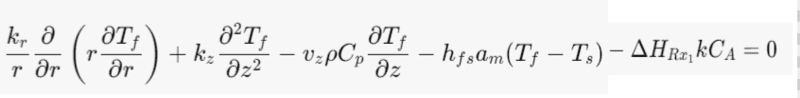
Does the catalyst transfer heat from the heat of homogeneous reaction to the fluid and surrounding. In a similar way the fluid phase undergoes a homogeneous reaction where heat is transfer to the catalyst and surrounding.
Where kr- thermal conductivity in the radial direction [W/(m*C)]
kz- thermal conductivity in the axial direction [W/(m*C)]
ρ- Bulk density [kg/m^3]
Cp- specific heat capacity [J/(Kg*C)]
HRx1- Heat of homogeneous reaction [J/mol]
hfs-solid-fluid heat transfer coefficient
Energy balance for the solid phase:
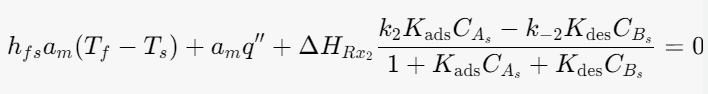
I think I am account for the heat of heterogeneous reaction twice but I am not sure.
HRx2- Heat of Heterogeneous reaction
q''- Electric heat flux
Boundary Conditions (Danckwert Conditions)
I am not so sure about the energy boundary conditions the heat flux at the wall equals the electric heat flux. Is this heat flux compensating the heat flux from both fluid phase and solid phase.
Species fluid and solid phase balances for a tubular reactor in which there is a homogeneous first order reaction and a heterogeneous reaction on the external surface of non-porous catalyst coated along the reactor wall.
Mole balance equation for the fluid phase
The heterogeneous reaction is represent by mass transfer to the solid phase.
Where Dr-radial diffusion coefficient
Dz- Axial diffusion coefficient [m^2/s]
vz- superficial fluid velocity [m/s]
km- mass transfer coefficient [m/s]
am- particle surface area per unit bed volume [m^-1]
k-rate constant [s^-1]
Solid Mole balance equation for the solid phase
Rs- heterogeneous rate of reaction (LHHW)
1)A+S⇌A-S (chemisorption of A)
2)A-S⇌B-S (Surface reaction)
3) B-S⇌B+S (Desorption of B)
2) is the rate determining reaction and 1) and 3) are assumed to be in equilibrium.
There is a single type of site and there is competitive adsorption between A and B.
The rate of adsorption is given by
At equilibrium the net rate of adsorption and desorption are 0. Therefore the surface coverage by A and B are given by.
where θv is the fraction of vacant sites.
Site balance:
Substitute into the rate determining step (rate equation):
We can simplify the above equation using the equilibrium constant for the heterogeneous reaction. At equilibrium the surface reaction is equal to 0.
Kads- [m^3/mol]
Kdes- [m^3/mol]
k2 -[mol/(m^3*s)]
Energy Balance for the fluid phase:
Does the catalyst transfer heat from the heat of homogeneous reaction to the fluid and surrounding. In a similar way the fluid phase undergoes a homogeneous reaction where heat is transfer to the catalyst and surrounding.
Where kr- thermal conductivity in the radial direction [W/(m*C)]
kz- thermal conductivity in the axial direction [W/(m*C)]
ρ- Bulk density [kg/m^3]
Cp- specific heat capacity [J/(Kg*C)]
HRx1- Heat of homogeneous reaction [J/mol]
hfs-solid-fluid heat transfer coefficient
Energy balance for the solid phase:
I think I am account for the heat of heterogeneous reaction twice but I am not sure.
HRx2- Heat of Heterogeneous reaction
q''- Electric heat flux
Boundary Conditions (Danckwert Conditions)
I am not so sure about the energy boundary conditions the heat flux at the wall equals the electric heat flux. Is this heat flux compensating the heat flux from both fluid phase and solid phase.
Last edited: