JD_PM
- 1,125
- 156
- TL;DR
- I want to understand why some branching ratios (BRs) are greater than others and discuss some other features of the attached plot. Besides, I want to figure out the Feynman diagrams (FDs) I do not find in the literature.
I will bold the ideas I would like to discuss so that they are easier to identify.
Hi everyone!
I am studying Higgs phenomenology, in particular its BRs
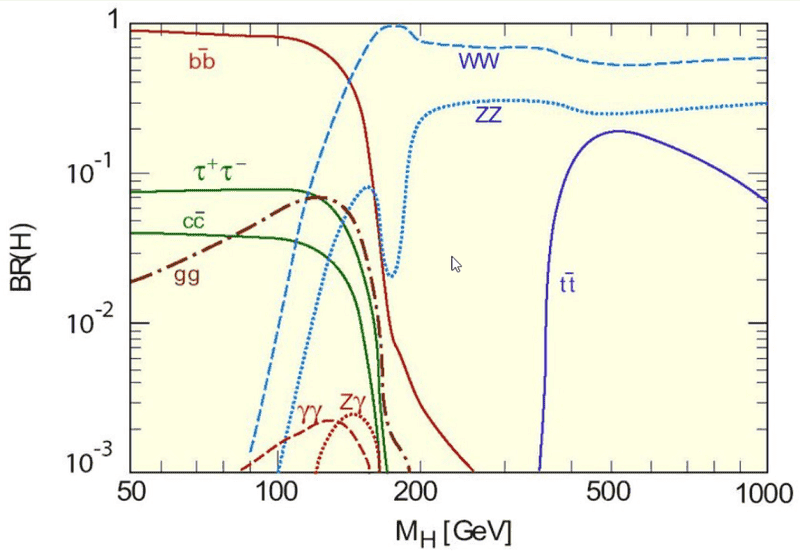

My line of reasoning is this: I first had a look at the decays where the Higgs particle couples directly (i.e. without intermediate particles) to the products; those are ##H^0 \to b \bar b, \ H^0 \to \tau \bar \tau## and ##H^0 \to c \bar c \ ## (##H^0 \to t \bar t## is of course not allowed due to conservation of energy; the top quark is about ##t \approx 172 \ GeV## while ##H^0 \approx 125 \ GeV##). Given that the coupling constant is ##m/v##, where the vacuum expectation value is given by ##v \approx 246 \ GeV##, it makes sense to think that the more massive the particle is the stronger it couples to the Higgs particle. Indeed, for those three ratios that argument seems to hold. Do you think it is OK?
Here comes the fun.
Once intermediate particles come into play I do not really understand why some channels have greater BRs than others. Next, let us look at the "massless" channels ##H^0 \to \gamma \gamma, \ H^0 \to gg##. I studied the golden channel ##H^0 \to \gamma \gamma## (Mandl & Shaw, page 446)

OK so W boson and quarks (only the top quark couples significantly to ##H^0## though) are the intermediators.
I struggle to find information in the literature regarding the decay channel ##H^0 \to gg##. I looked up Higgs decay to gluon in Google Scholar and checked the first five but found no (modern i.e. not in terms of ) FD. One could guess and say "well, the gluon is massless as well so we could expect to have the exact same diagrams that for ##H^0 \to \gamma \gamma##" (this is actually the same guess a PF user made back in 2014). I do not think this is right, as the BRs differ quite significantly so I expect the associated FDs to differ as well. Hence
What are the FDs associated to ##H^0 \to gg## and why does its BR differ that significantly with ##H^0 \to \gamma \gamma## (despite both products being massless)?
Regarding FDs, I have the same issue with the channel ##H^0 \to Z \gamma##: I do not find them in the literature.
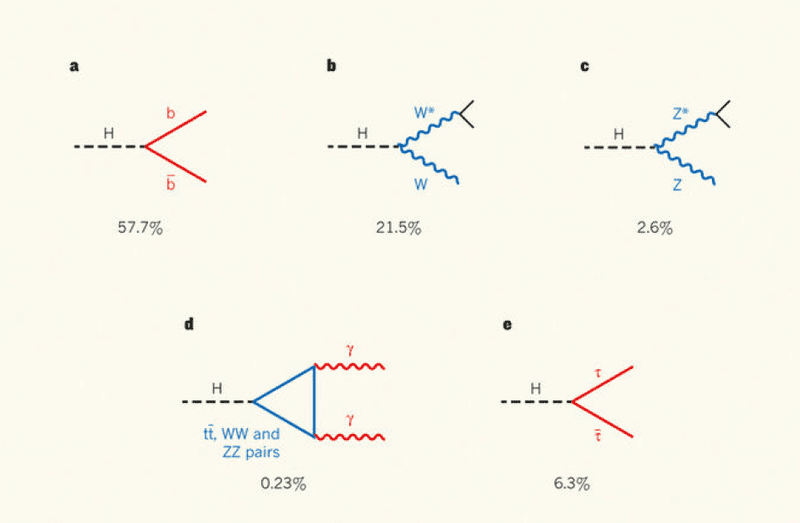
Finally, let me comment on the last two channels: ##H^0 \to W W^*## and ##H^0 \to Z Z^*##. I have studied they have essentially the same FD (b and c below)
My argument to explain their difference in BRs is based on their coupling constants: we know that the Higgs particle couples to W and Z bosons as follows

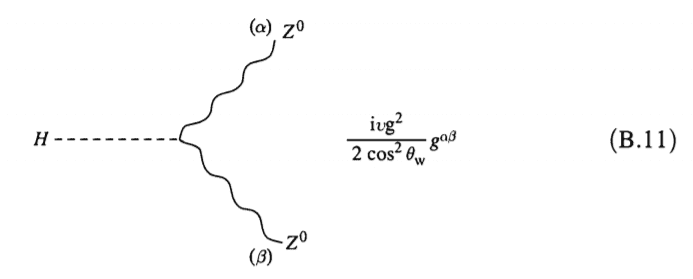
We also know that ##M_W^2 = \frac{g^2v^2}{4}## and ##M_Z^2 = \frac{g^2v^2}{4 \cos \theta_W}## so we deduce that the ##HWW## coupling goes as ##M^2_W/v## whereas the ##HZZ## coupling goes as ##M^2_Z/v##. Hence this reasoning leads to think that we should expect a greater BR for Z.
This is wrong and by far... How to explain their BR then?
Last comment: in the plot we observe a sudden minimum in ZZ... why?
I appreciate to discuss with you all
Thank you!
I am studying Higgs phenomenology, in particular its BRs
My line of reasoning is this: I first had a look at the decays where the Higgs particle couples directly (i.e. without intermediate particles) to the products; those are ##H^0 \to b \bar b, \ H^0 \to \tau \bar \tau## and ##H^0 \to c \bar c \ ## (##H^0 \to t \bar t## is of course not allowed due to conservation of energy; the top quark is about ##t \approx 172 \ GeV## while ##H^0 \approx 125 \ GeV##). Given that the coupling constant is ##m/v##, where the vacuum expectation value is given by ##v \approx 246 \ GeV##, it makes sense to think that the more massive the particle is the stronger it couples to the Higgs particle. Indeed, for those three ratios that argument seems to hold. Do you think it is OK?
Here comes the fun.
Once intermediate particles come into play I do not really understand why some channels have greater BRs than others. Next, let us look at the "massless" channels ##H^0 \to \gamma \gamma, \ H^0 \to gg##. I studied the golden channel ##H^0 \to \gamma \gamma## (Mandl & Shaw, page 446)
OK so W boson and quarks (only the top quark couples significantly to ##H^0## though) are the intermediators.
I struggle to find information in the literature regarding the decay channel ##H^0 \to gg##. I looked up Higgs decay to gluon in Google Scholar and checked the first five but found no (modern i.e. not in terms of ) FD. One could guess and say "well, the gluon is massless as well so we could expect to have the exact same diagrams that for ##H^0 \to \gamma \gamma##" (this is actually the same guess a PF user made back in 2014). I do not think this is right, as the BRs differ quite significantly so I expect the associated FDs to differ as well. Hence
What are the FDs associated to ##H^0 \to gg## and why does its BR differ that significantly with ##H^0 \to \gamma \gamma## (despite both products being massless)?
Regarding FDs, I have the same issue with the channel ##H^0 \to Z \gamma##: I do not find them in the literature.
Finally, let me comment on the last two channels: ##H^0 \to W W^*## and ##H^0 \to Z Z^*##. I have studied they have essentially the same FD (b and c below)
My argument to explain their difference in BRs is based on their coupling constants: we know that the Higgs particle couples to W and Z bosons as follows
We also know that ##M_W^2 = \frac{g^2v^2}{4}## and ##M_Z^2 = \frac{g^2v^2}{4 \cos \theta_W}## so we deduce that the ##HWW## coupling goes as ##M^2_W/v## whereas the ##HZZ## coupling goes as ##M^2_Z/v##. Hence this reasoning leads to think that we should expect a greater BR for Z.
This is wrong and by far... How to explain their BR then?
Last comment: in the plot we observe a sudden minimum in ZZ... why?
I appreciate to discuss with you all
Thank you!