- 2,355
- 10
Anamitra: still wrong after all these years
... it feels like years, anyway, and I'm not even talking to this poster directly, so you all have more fortitude than I!
"Anamitra": I'm reading that as one word, not "Ana Mitra". Unless you have reason to believe otherwise, I presume User:Anamitra is male. (In at least one post, he seems to sign himself " Anamitra Palit".) I have to say, I also think there is a good chance User:Anamitra is trolling PF, although I don't know what his motivation might be. But even if not, posters who are clueless in math/physics are often clueless regarding malware too, so especially likely to pass on a nasty infection. So I wouldn't open any pdfs from User:Anamitra under any circumstances--- pdf is one of the most common vectors for malware of all kinds, and to some extent the dangers are platform independent. 'Nuff said.
Some quick comments on Anamitra's post:
He is using +--- signature and pointlessly putting m=1/2, but I'll use -+++ signature and write
<br /> ds^2 = -(1-2m/r) \, dt^2 + \frac{dr^2}{1-2m/r} + r^2 \, d\Omega^2<br />
Then he considers the signature -++ submanifold r=r_0, where r_0 > 2m (a coordinate cylinder in the Schwarzschild chart in the exterior region, if you like):
<br /> ds^2 = -(1-2m/r) \, dt^2 + r_0^2 \, d\Omega^2<br />
Then he appears to claim that a coordinate transformation takes this to the cartesian form
<br /> ds^2=dT^2 - dx^2-dy^2<br />
But this would only be possible if the coordinate hypercylinder r=r_0 has vanishing curvature tensor, since only a locally flat manifold can be given such a cartesian chart. But this submanifold actually has nonzero curvature tensor (easily checked with Ctensor under Maxima or GRTensorII under Maple). So, he's already made a fatal error. (He seems to think that because r=r_0 appears in the Schwarzschild chart as a "hypercylinder", it is locally flat, but that is wrong.)
In his other remarks, he seems to think he is constructing a path and parallel transporting a frame along a path, but seems confused about what the -++ submanifold r=r_0 has to do with that, and in any case, he clearly has no idea how to work with covariant derivatives.
So Anamitra is doing this all wrong, but to be fair, when I looked over some well known textbooks hoping for a quick cite, I found that none of them say very much about how to do parallel transport in practice! So I've added this to my to do list for the BRS.
That's the idea, yes! In particular, it suffices to say how to parallel transport any frame vector along a given path, in order to know how to parallel transport any vector along that path. The connection one-form is defined exactly to say how to parallel transport the frame vectors along any path.
Until I can try to explain this properly, some remarks off the top of my head:
Ultimately, parallel transport of a vector \vec{X} \in T_p M based at some point p along a timelike or spacelike curve with unit tangent vector \vec{U} amounts to solving an initial value problem
<br /> \nabla_{\vec{U}} \vec{X} = 0, \; \; \vec{X}(0) = \vec{X}_p<br />
That should make us think of integrating a one-form taking values in a Lie algebra, which upon exponentiation gives an element in a Lie group. In a Riemannian n-fold, this Lie group is SO(n), and in a Lorentzian 4-fold, it is SO_+(1,3). (These are simply connected Lie groups.) That is, we should think of an element of so(n) as an "infinitesimal rotation" and an element of so(1,n-1) as an "infinitesimal boost/rotation", whose exponential is an element of the proper orthochronous Lorentz group.
Pursuing this line of thought leads to a picture of (in the Riemannian case) an SO(n)-bundle over M, in which the connection tells how to move "vertically" along the fibers as we move along a curve in the base space M. See figure below, and see Chapter 7 of Isham, Modern Differential Geometry for Physicists, World Scientific, 1999.
As you would probably expect, following Elie Cartan, I claim that the easiest way of computing parallel transport in practice is to use frame fields. In textbooks which discuss frame fields in just enough detail to make them seem like inscrutable beasts, but not enough detail to reveal them as the simple-minded creatures they really are*, you'll see that the usual expression for the Levi-Civita connection in terms of a coordinate basis (an alternating sum of three first derivatives of the metric) must be supplemented by another three terms. This makes things look more complicated, but it is only because when we define a frame field, we have the freedom to choose how to rotate the frame as we move smoothly from place to place. And we can use that freedom to simplify problems!
*Cite suppressed to protect the guilty? No, I just can't think of one right now!
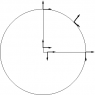
For example, in the familiar case of parallel transport of a frame around a spherical triangle covering an octant of the unit sphere (see the figure below), the standard frame
<br /> \begin{array}{rcl}<br /> \vec{e}_1 & = & \partial_\theta \\<br /> \vec{e}_2 & = & \frac{1}{\sin(\theta)} \; \partial_\phi<br /> \end{array}<br />
in the trig chart
<br /> ds^2 = d\theta^2 + \sin(\theta)^2 \, d\phi^2, \; \;<br /> 0 < \theta < \pi, \; -\pi < \phi < \pi <br />
is already parallel transported around the loop we want, with a mismatch at the origin where the frame (and the chart) is not defined. So in this case Cartan's structure equation
<br /> d\vec{e}_k = \vec{e}_j \, {\omega^j}_k<br />
(think right multiplication of a row vector by a matrix), which says how to parallel transport the frame vectors using the connection one-forms--- in our example we have only one to worry about, {\omega^1}_2 = -\cos(\theta) \; d\phi--- says "just follow the frame!"
(I realize that sounds just a bit like what Anamitra may have been trying to say, but I really don't see how to massage his post into a munged version of what I just said.)
We should really think of the "connection one-forms" as a single one-form taking values in the Lie algebra so(n), or in our example so(2):
<br /> \left[ \begin{array}{cc} <br /> 0 & -\cos(\theta) \, d\phi \\<br /> \cos(\theta) \, d\phi & 0<br /> \end{array} \right]<br />
Then, in our simple example, \phi is constant on the first and third arcs, and the cosine vanishes on the equator. Even though we didn't rotate wrt the frame vectors as we traveled around this clockwise arc, since the frame itself has a mismatch at the origin (by construction), the result is a net clockwise rotation by one quarter turn. Which happens to agree (not by chance!) with the result of integrating the constant curvature one over the spherical triangle!
In a slightly more elaborate example, apparently the one Anamitra had in mind, replace the middle arc by a nongeodesic arc on the latitude \theta=\pi/4 and shorten the first and last arcs appropriately (strictly speaking, no longer a spherical triangle because one side is not a geodesic arc). Then the cosine factor is a nonzero constant on that arc, and we can integrate to obtain a nonzero counterclockwise rotation by a certain fraction of a quater turn wrt the frame vectors. The result when we transport a vector around in the new clockwise closed loop is a net clockwise rotation by another fraction of a quarter turn.
So in the example of the unit sphere using trig chart, the connection one-form {\omega^1}_2 = -\cos(\theta) \, d\phi is telling us that the given frame is parallel transported when we move along radial lines (great circle arcs) and also when we move along the equator (also a great circle arc), but when we move along a general latitude (not a geodesic arc), we have a rotation rate given by exponentiating an element of the Lie algebra so(2) to obtain an element of the Lie group SO(2).
In a positively curved surface, parallel transport around a clockwise loop results in a clockwise rotation. In a negatively curved surface, parallel transport around a clockwise loop results in a counter-clockwise rotation. In a surface with curvature positive in some places and negative in others, you have to integrate the curvature over the region bounded by the loop, using the appropriate volume form, to see which sign wins.
If I am making this sound hard, that is only because I haven't yet thought very hard about how to explain it!
I recommend Flanders, Differential Forms with Applications to the Physical Sciences, Dover reprint, org. published 1963, even though Flanders doesn't mention the formula I referred to above, because this book offers a brief and intuitive introduction.
I can't resist adding that in Cartanian geometry, the common generalization of Riemannian geometry and Kleinian geometry, we allow more interesting fibers than just SO(n) (Riemannian geometry) or SO(1,n-1) (Lorentzian geometry). For example, we can allow the group G in our G-bundle to include euclidean homotheties as well as rotations. Then parallel transport in a loop can result in a vector coming back rescaled as well as rotated! That was pretty much Weyl's original gauge theory, introduced as a (failed) attempt to unify classical electromagnetism and gtr. We also obtain a notion of the curvature of a connection which gives an appropriate notion of "locally flat" manifold for such a G-geometry.
Figures (left to right):
... it feels like years, anyway, and I'm not even talking to this poster directly, so you all have more fortitude than I!
"Anamitra": I'm reading that as one word, not "Ana Mitra". Unless you have reason to believe otherwise, I presume User:Anamitra is male. (In at least one post, he seems to sign himself " Anamitra Palit".) I have to say, I also think there is a good chance User:Anamitra is trolling PF, although I don't know what his motivation might be. But even if not, posters who are clueless in math/physics are often clueless regarding malware too, so especially likely to pass on a nasty infection. So I wouldn't open any pdfs from User:Anamitra under any circumstances--- pdf is one of the most common vectors for malware of all kinds, and to some extent the dangers are platform independent. 'Nuff said.
Some quick comments on Anamitra's post:
He is using +--- signature and pointlessly putting m=1/2, but I'll use -+++ signature and write
<br /> ds^2 = -(1-2m/r) \, dt^2 + \frac{dr^2}{1-2m/r} + r^2 \, d\Omega^2<br />
Then he considers the signature -++ submanifold r=r_0, where r_0 > 2m (a coordinate cylinder in the Schwarzschild chart in the exterior region, if you like):
<br /> ds^2 = -(1-2m/r) \, dt^2 + r_0^2 \, d\Omega^2<br />
Then he appears to claim that a coordinate transformation takes this to the cartesian form
<br /> ds^2=dT^2 - dx^2-dy^2<br />
But this would only be possible if the coordinate hypercylinder r=r_0 has vanishing curvature tensor, since only a locally flat manifold can be given such a cartesian chart. But this submanifold actually has nonzero curvature tensor (easily checked with Ctensor under Maxima or GRTensorII under Maple). So, he's already made a fatal error. (He seems to think that because r=r_0 appears in the Schwarzschild chart as a "hypercylinder", it is locally flat, but that is wrong.)
In his other remarks, he seems to think he is constructing a path and parallel transporting a frame along a path, but seems confused about what the -++ submanifold r=r_0 has to do with that, and in any case, he clearly has no idea how to work with covariant derivatives.
So Anamitra is doing this all wrong, but to be fair, when I looked over some well known textbooks hoping for a quick cite, I found that none of them say very much about how to do parallel transport in practice! So I've added this to my to do list for the BRS.
Dalespam said:Without knowing better, the way I would approach it would be to construct an orthonormal basis at the beginning of the path and then parallel transport those basis vectors along the path. That way, at any point along the path you would have a set of basis vectors which define a coordinate system where parallel transported vectors have constant components, as well as an easy way to transform back to the original coordinates.
That's the idea, yes! In particular, it suffices to say how to parallel transport any frame vector along a given path, in order to know how to parallel transport any vector along that path. The connection one-form is defined exactly to say how to parallel transport the frame vectors along any path.
Until I can try to explain this properly, some remarks off the top of my head:
Ultimately, parallel transport of a vector \vec{X} \in T_p M based at some point p along a timelike or spacelike curve with unit tangent vector \vec{U} amounts to solving an initial value problem
<br /> \nabla_{\vec{U}} \vec{X} = 0, \; \; \vec{X}(0) = \vec{X}_p<br />
That should make us think of integrating a one-form taking values in a Lie algebra, which upon exponentiation gives an element in a Lie group. In a Riemannian n-fold, this Lie group is SO(n), and in a Lorentzian 4-fold, it is SO_+(1,3). (These are simply connected Lie groups.) That is, we should think of an element of so(n) as an "infinitesimal rotation" and an element of so(1,n-1) as an "infinitesimal boost/rotation", whose exponential is an element of the proper orthochronous Lorentz group.
Pursuing this line of thought leads to a picture of (in the Riemannian case) an SO(n)-bundle over M, in which the connection tells how to move "vertically" along the fibers as we move along a curve in the base space M. See figure below, and see Chapter 7 of Isham, Modern Differential Geometry for Physicists, World Scientific, 1999.
As you would probably expect, following Elie Cartan, I claim that the easiest way of computing parallel transport in practice is to use frame fields. In textbooks which discuss frame fields in just enough detail to make them seem like inscrutable beasts, but not enough detail to reveal them as the simple-minded creatures they really are*, you'll see that the usual expression for the Levi-Civita connection in terms of a coordinate basis (an alternating sum of three first derivatives of the metric) must be supplemented by another three terms. This makes things look more complicated, but it is only because when we define a frame field, we have the freedom to choose how to rotate the frame as we move smoothly from place to place. And we can use that freedom to simplify problems!
*Cite suppressed to protect the guilty? No, I just can't think of one right now!
For example, in the familiar case of parallel transport of a frame around a spherical triangle covering an octant of the unit sphere (see the figure below), the standard frame
<br /> \begin{array}{rcl}<br /> \vec{e}_1 & = & \partial_\theta \\<br /> \vec{e}_2 & = & \frac{1}{\sin(\theta)} \; \partial_\phi<br /> \end{array}<br />
in the trig chart
<br /> ds^2 = d\theta^2 + \sin(\theta)^2 \, d\phi^2, \; \;<br /> 0 < \theta < \pi, \; -\pi < \phi < \pi <br />
is already parallel transported around the loop we want, with a mismatch at the origin where the frame (and the chart) is not defined. So in this case Cartan's structure equation
<br /> d\vec{e}_k = \vec{e}_j \, {\omega^j}_k<br />
(think right multiplication of a row vector by a matrix), which says how to parallel transport the frame vectors using the connection one-forms--- in our example we have only one to worry about, {\omega^1}_2 = -\cos(\theta) \; d\phi--- says "just follow the frame!"
(I realize that sounds just a bit like what Anamitra may have been trying to say, but I really don't see how to massage his post into a munged version of what I just said.)
We should really think of the "connection one-forms" as a single one-form taking values in the Lie algebra so(n), or in our example so(2):
<br /> \left[ \begin{array}{cc} <br /> 0 & -\cos(\theta) \, d\phi \\<br /> \cos(\theta) \, d\phi & 0<br /> \end{array} \right]<br />
Then, in our simple example, \phi is constant on the first and third arcs, and the cosine vanishes on the equator. Even though we didn't rotate wrt the frame vectors as we traveled around this clockwise arc, since the frame itself has a mismatch at the origin (by construction), the result is a net clockwise rotation by one quarter turn. Which happens to agree (not by chance!) with the result of integrating the constant curvature one over the spherical triangle!
In a slightly more elaborate example, apparently the one Anamitra had in mind, replace the middle arc by a nongeodesic arc on the latitude \theta=\pi/4 and shorten the first and last arcs appropriately (strictly speaking, no longer a spherical triangle because one side is not a geodesic arc). Then the cosine factor is a nonzero constant on that arc, and we can integrate to obtain a nonzero counterclockwise rotation by a certain fraction of a quater turn wrt the frame vectors. The result when we transport a vector around in the new clockwise closed loop is a net clockwise rotation by another fraction of a quarter turn.
So in the example of the unit sphere using trig chart, the connection one-form {\omega^1}_2 = -\cos(\theta) \, d\phi is telling us that the given frame is parallel transported when we move along radial lines (great circle arcs) and also when we move along the equator (also a great circle arc), but when we move along a general latitude (not a geodesic arc), we have a rotation rate given by exponentiating an element of the Lie algebra so(2) to obtain an element of the Lie group SO(2).
In a positively curved surface, parallel transport around a clockwise loop results in a clockwise rotation. In a negatively curved surface, parallel transport around a clockwise loop results in a counter-clockwise rotation. In a surface with curvature positive in some places and negative in others, you have to integrate the curvature over the region bounded by the loop, using the appropriate volume form, to see which sign wins.
If I am making this sound hard, that is only because I haven't yet thought very hard about how to explain it!
I recommend Flanders, Differential Forms with Applications to the Physical Sciences, Dover reprint, org. published 1963, even though Flanders doesn't mention the formula I referred to above, because this book offers a brief and intuitive introduction.
I can't resist adding that in Cartanian geometry, the common generalization of Riemannian geometry and Kleinian geometry, we allow more interesting fibers than just SO(n) (Riemannian geometry) or SO(1,n-1) (Lorentzian geometry). For example, we can allow the group G in our G-bundle to include euclidean homotheties as well as rotations. Then parallel transport in a loop can result in a vector coming back rescaled as well as rotated! That was pretty much Weyl's original gauge theory, introduced as a (failed) attempt to unify classical electromagnetism and gtr. We also obtain a notion of the curvature of a connection which gives an appropriate notion of "locally flat" manifold for such a G-geometry.
Figures (left to right):
- Schematic picture of parallel transport in the bundle picture (Riemannian case): fibers are copies of SO(n), base space is Riemannian manifold (M,g), parallel transport in a loop generally results in a nonzero rotation of a vector carried around the loop.
- Simple example of parallel transport of a frame around a loop on unit sphere
- segment (great circle arc) \phi=\pi/2[/tex] from origin to \theta=\pi/2, \; \phi=\pi/2<br /> [*] quarter circle arc on equator (great circle arc)<br /> [*] segment (great circle arc) back to origin<br />
Attachments
Last edited: