Recapitulation: Overview of the LTB dusts
This will be a bit sketchy; for details see Chapter 18 of Jerzy Plebanski and Andrzej Krasinski, An Introduction to General Relativity and Cosmology, Cambridge University Press, 2006. This book is IMO
essential reading for anyone studying cosmology at the graduate level, not to mention working cosmologists. I can't recommend it too highly!
The basic idea of the LTB dusts is due to Lemaitre 1933: consider a dust (pressureless perfect fluid) which consists of nested spherical shells, such that each shell has homogeneous mass density, but shells can shrink over time, and the density can vary between shells. This led Lemaitre to introduce the comoving chart
<br />
ds^2 = -dt^2 + \frac{(R^\prime)^2}{1+2\,\epsilon} \; dr^2 + R^2 \; \left( d\theta^2 + \sin(\theta)^2 \, d\phi^2 \right)<br />
where \epsilon is a function of r only and R is a function of t,r, and where it will be convenient to denote time derivatives by overdots, and r derivatives by primes. Then computing the Einstein tensor wrt the frame I gave earlier and requiring all but G^{11} to vanish makes this the frame of the dust and also leads to a constraint equation
<br />
\ddot{R} = \frac{2 \, \epsilon - \dot{R}^2}{2 \, R}<br />
which can be integrated once to give a first order PDE:
<br />
\dot{R}^2/2 = \frac{m}{R} + \epsilon<br />
where m is a new function of r only. This is formally identically to the equation of radial motion of a test particle moving in a Coulomb field in Newtonian gravitation, and then \epsilon(r_0) is the specific energy (energy per unit mass) of the test particle, an invariant of the motion for any particle in the shell r=r_0, and the first term is (the negative of) the Newtonian gravitational potential. Thus, for a given shell r=r_0 we make the following interpretations:
- m(r_0) is the active mass inside the shell,
- \epsilon(r_0) is the energy of the shell;
- negative energy shells are bounded (expand and recollapse),
- zero energy shells are marginally bound
- positive energy shells are unbound
- A = 4 \pi \; R(t_0, r_0)^2 is the surface area of the shell at t=t_0
The coordinate r simply labels the shells, so it can go negative as long as R remains nonnegative. In many LTB dust solutions, r=0 will correspond to the world line of an axis of spherical symmetry, but this typically does not exist for all times. Also, differences in t along the world line of a dust particle (vertical constant lines, i.e. constant angular and radial coordinates) correspond to elapsed proper time, so R and the angular coordinates have immediate geometric significance, and t has direct physical significance.
Later workers noticed that one can easily generalize to other shell geometries, obtaining the same constraint equation, with the same interpretations! (Except for the bit about surface area of the shells, which need no longer be compact.) In particular, we can consider cylindrical shells (with \mathbb{R} \times S^1 geometry):
<br />
ds^2 = -dt^2 + \frac{(R^\prime)^2}{2\,\epsilon} \; dr^2 + R^2 \; \left( dz^2 + d\phi^2 \right)<br />
and pseudospherical shells (with H^2 geometry):
<br />
ds^2 = -dt^2 + \frac{(R^\prime)^2}{-1+2\,\epsilon} \; dr^2 + R^2 \; \left( d\theta^2 + \sinh(\theta)^2 \, d\phi^2 \right)<br />
(Notice that we require \epsilon > -1/2, \; \epsilon > 0, \; \epsilon > 1/2, for spherical, cylindrical, and pseudospherical shells respectively.) Then the spacetime globally organizes the geometry of the "nested" shells such that we have a three-dimensional Lie algebra of spacelike Killing vector fields, corresponding respectively to the Lie groups
- SO(3) acting on the nested spherical shells,
- E(3) acting on the nested planar shells (or, locally, on nested cylindrical shells),
- SO(2,1) acting on the nested pseudospherical shells
In all cases, the density of the dust is simply
<br />
\mu = \frac{m^\prime/R^\prime}{4 \pi \, R^2}<br />
where in the case of spherical shells, we can interpret the denominator as the surface area of a shell.
We should think of the constraint like this: we choose two functions of one variable, m, \; \epsilon and then solve to find R. (Indeed, from the interpretation, we should think of m as a given non-negative function of r.) From the form of the constraint, we should expect that the solution should involve specifying a third function of r only, b. Indeed, we can solve for R implicitly in the form
<br />
t - b = \frac{\pm R^{3/2}}{\sqrt{2 m}} F\left( \frac{-\epsilon \, R}{m} \right)<br />
where we choose the minus sign for expanding shells and the plus sign for contracting shells, and where
<br />
F(\xi) = \begin{cases}<br />
\xi^{-3/2} \; \operatorname{arcsin}(\sqrt{\xi}) - \frac{\sqrt{1-\epsilon}}{\xi} & 0 < \xi \leq 1 \\<br />
2/3 & \xi = 0 \\<br />
-(-\xi)^{-3/2} \; \operatorname{arcsinh}(\sqrt{-\xi}) - \frac{\sqrt{1-\epsilon}}{\xi} & -\infty < \xi < 0<br />
\end{cases}<br />
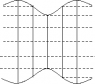
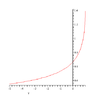
Here, F is positive, increasing, convex, bounded, smooth function defined on (-\infty, 1], with range(0,\pi/2] (see the plot below), so the inverse function exists. In fact, we put G(\xi) = \xi^{3/2} \; F(\xi) and consider its inverse as a special function with known properties, we can solve for R in closed form as a function of the three (almost) arbitrarily chosen functions m, \, \epsilon, \, b. Thus, the Riemann wealth of LTB dusts is, crudely, "three functions of one variable"; this might include some gauge transformations among different LTB representations of the same spacetime plus matter density/flow. However, the form of the Lemaitre chart is quite restrictive, as noted above, so it is reasonable to hope that it is essentially a canonical chart for LTB dusts.
The eigenvalues of the Riemann tensor turn out to consist of
- two simple eigenvalues 2 \, m/R^3, \; 2 \, m/R^3 - m^\prime/R^\prime/R^2
- two double eigenvalues -m/R^3, \; -m/R^3 + m^\prime/R^\prime/R^2
From these expressions, we can see that there are two ways the curvature can blow up:
- R = 0 when m > 0,
- R^\prime = 0 when m^\prime \neq 0
The first of these possibilities corresponds to something familiar from FRW dusts: initial and/or final singularities, which are strong and spacelike. The second is something new: shell-crossing singularities, where the density of the dust blows up--- more about that later.
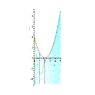
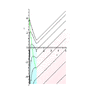
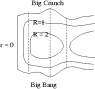
Suppose you have found a solution R(t,r) to the constraint equation. To visualize the dynamics, use the spherical symmetry to suppress the angular coordinates, and plot contours of R wrt t,r, with the boundaries of the singular locus R=0. Also plot the shell-crossing singularities, if any. Plot some world sheets of shells of dust particles as vertical line segments
- between initial and final singularities (if the shell has negative energy)
- above an initial singularity or below a final singularity (if it has zero or positive energy)
Then you can see how each shell expands and contracts by looking at which contours of R it crosses. (See the figure below.)
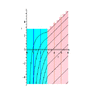
Suppose that R=0 and m=0 at r=0, so that r=0 is a center of spherical symmetry. Then the principle outgoing null geodesic congruence consist of all null geodesics which go out from r=0; it has spherical wavefronts which "want" to expand (but in a black hole interior, wind up contracting). The principle ingoing null geodesic congruence consist of all null geodesics which go into r=0. From the line element you can see how to plot the world sheets of these expanding or contracting spherical wavefronts in our picture, so you can plot some of them too for additional insight.
In more detail, the principle outgoing null geodesic congruence has the form
<br />
\vec{k} = f \, \left( \partial_t + \frac{\sqrt{1+2 \, \epsilon}}{R^\prime} \, \partial_r \right)<br />
where f is an undetermined function of t,r. Computing the acceleration and requiring this to vanish gives an equation on f which cannot be solved easily, but computing the expansion scalar using this equation as a constraint, we can verify that the shear and twist scalars vanish identically, so that this congruence really is expanding or contracting spherically. Even better, f factors out from the expression we find for the expansion, so we can compute the locus where the expansion scalar vanishes, which turns out to be R = 2 \, m, which defines implicity a locus, a certain submanifold. That is, if our dust includes region containing negative energy shells which collapse to form a black hole, the world sheets encounter a future apparent horizon where the expansion scalar of the principle outgoing null geodesic congruence changes sign from positive to negative (the expansion scalar of the ingoing congruence is remains negative). This is, by definition, an apparent horizon. Pictorially, it is the locus where the contours of R become tangent to the world sheets of the spherical wavefronts of the outgoing null geodesic congruence (increasing surface aera, so
expanding, below the AH; decreasing surface area, so
contracting above it, with the wavefronts ultimately collapsing to a Big Crunch final singularity).
Similar statements hold for the principle ingoing null geodesic congruence.
We can study the physical experience of observers riding on dust particles by computing some tensors wrt the frame of the dust (case of an LTB dust with spherical shells):
<br />
\begin{array}{rcl}<br />
\vec{e}_1 & = & \partial_t \\<br />
\vec{e}_2 & = & \frac{R^\prime}{\sqrt{1+2 \, \epsilon}} \; \partial_r \\<br />
\vec{e}_3 & = & \frac{1}{R} \; \partial_\theta \\<br />
\vec{e}_4 & = & \frac{1}{R \, \sin(\theta)} \; \partial_\phi<br />
\end{array}<br />
The acceleration vector vanishes (as it must, since the dust particles feel no forces, in particular, no pressure). So does the vorticity tensor, so the timelike geodesic congruence defined by \vec{U} = \vec{e}_1 is hypersurface orthogonal, and the unique family of hyperslices orthogonal to the world lines of the dust particles are the coordinate planes t=t_0 in the Lemaitre chart. The expansion tensor is diagonal with
<br />
\begin{array}{rcl}<br />
H_{22} & = & \frac{-m/R^2 + m^\prime/R^\prime/R + \epsilon^\prime/R^\prime}{\dot{R}} \\<br />
H_{33} & = & H_{44} = \frac{\dot{R}}{R}<br />
\end{array}<br />
The electroriemann tensor is diagonal with
<br />
\begin{array}{rcl}<br />
E_{22} & = & \frac{-2m}{R^3} + \frac{m^\prime/R^\prime}{R^2} \\<br />
E_{33} & = & E_{44} = \frac{m}{R^3}<br />
\end{array}<br />
and the magnetoriemann tensor vanishes identically (no spinning sources). The three dimensional Riemann tensor of the hyperslices is
<br />
\begin{array}{rcl}<br />
r_{2323} & = & r_{2424} = \frac{-\epsilon^\prime/R^\prime}{R} \\<br />
r_{3434} & = & \frac{-2\, \epsilon}{R^2}<br />
\end{array}<br />
The only nonzero component of the Einstein tensor is of course G^{11} = 8 \pi \; \mu.
If we set \epsilon=0, as a special case of the implicit solution above we obtain the explicit solution
<br />
R = \begin{cases}<br />
( 9\,m/2 )^{1/3} \; ( t - b )^{2/3} & \rm{expanding \; shells} \\<br />
( 9\,m/2 )^{1/3} \; ( b - t )^{2/3} & \rm{contracting \; shells}<br />
\end{cases}<br />
where b gives the coordinate time at which the initial or final singularity occurs, for each shell. This defines the class of LTB dusts in which all the shells have zero energy, i.e. the hyperslices are locally flat. This class of LTB dusts turns out to be too restrictive, in the sense that doesn't exhibit any of the really interesting behavior! (The wealth of this class is only two functions of one variable.) As a special case, m = k \; r^3 and b = b_0 recovers the (expanding) FRW dust with E^3 hyperslices. Similarly, we can ask when the spatial hyperslices are uniformly curved with S^3 or H^3 geometry. This leads to an equation which can be solved to recover the FRW dusts with S^3 or H^3 geometry. And when \epsilon is constant, we should have slices with \mathbb{R} \times S^2 topology (not geometry, unless R has the form R=r \, f(t)).
Another important special case: any region r_1 < r < r_2 where m is constant is a
vacuum region, and because it is spherically symmetric, this must be a portion of the Schwarzschild vacuum. Now the dust congruence is no longer priviliged, but it is still an inertial congruence corresponding to a spherically symmetric family of radially ingoing or outgoing observers. If we choose \epsilon = 0, so that the orthogonal hyperslices are locally flat, we recover the Lemaitre observers.
If R^\prime = 0 at some r=r_0, t=t_0, two nearby shells r= r_0-\delta, \; r= r_0 + \delta will have almost the same surface area, suggesting that shells are colliding, hence the name "shell-crossing singularity". The Lemaitre chart has a coordinate singularity at such loci, but we can change to a Gautreau chart (a generalized Painleve chart) and this clearly shows that, indeed, shell-crossing singularities occur when either
- outer shells are contracting faster than inner shells and overtake them, piling up to create a "density caustic",
- inner shells are expanding faster than outer shells and overtake them, again forming a density caustic.
(...to be continued)
Figures (left to right):
- Schematic picture of a region in an LTB dust containing a center of spherical symmetry surrounded by negative energy shells of dust, with angular coordinates suppressed. The center of spherical symmetry r=0 at left; initial singularity at bottom; final singularity at top. Contours R=1, R=2 shown with some world sheets of shells (dotted line segments), showing how some of the shells expand to larger sizes than others before recollapsing. Also, recalling that t corresponds to proper time along world lines of dust particles, some particles exist longer than others.
- Plot of the function F(\xi)