Buck Converter (Step Down Chopper Derivation)

[jaus tail]

Hi,
I'm studying Choppers and I'm struggling with derivation of Buck Converter.

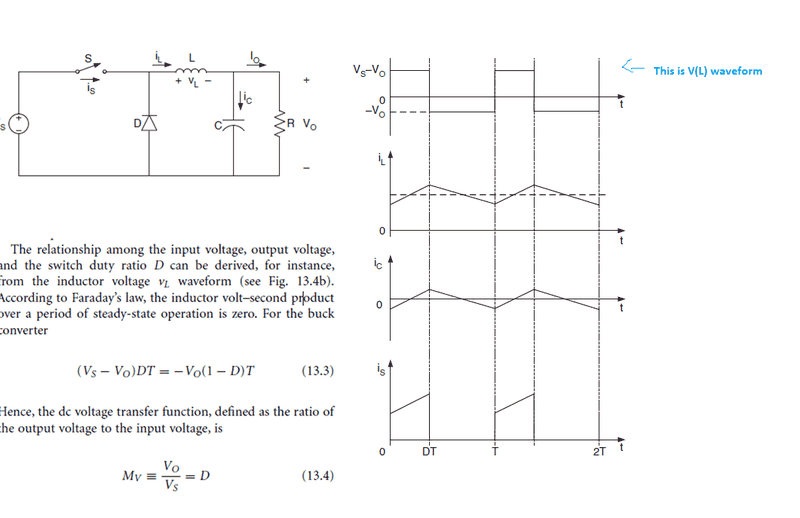
As per equation 13.3 if I solve it ahead I get
V_s D T - V_o D T = - V_o T + V_o D T
Solving this ahead I get
Vs (D T ) = Vo (-T + DT + DT)
Vs (DT) = Vo(2DT - T)
Vs D = Vo (2D - 1)
Vo / Vs = D/(2D - 1)
Not sure how to go ahead from here to reach equation 13.4

 

[the_emi_guy]

There is an error in 13.3. There is no minus sign in front of the Vo on the right-hand side.

You can catch these kinds of errors by visualizing what the equations are telling us physically.

 

[jaus tail]

But the graph also has - Vo.
Physically area means integrating of V and t.

 

[the_emi_guy]

The areas are equal. You can sum them to zero, one contributing positive, the other contributing negative. If they are on opposite sides of the equal sign they will both share the same sign (otherwise they aren't equal).

 

[jaus tail]

If they are on opposite sides of the equal sign they will both share the same sign (otherwise they aren't equal).

This is what I don't understand. If they are on opposite side why will both share same sign. Negative Y-axis has negative numbers.
Other book said average voltage for inductor is zero and then they've derived for step down chopper. So I got that through that method.
Like:
V(L during storing) + V(L during releasing) = 0
So (Vs - Vo) Ton - Vo * Toff = 0
This gives derivation.

 

[the_emi_guy]

As I said in my first post, you need to see the physical meaning of these equations.

Try putting in real numbers: Say it is a buck regulator dropping 10V down to 1V. Thus Vs = +10V and Vo=+1V.
Where does that lead?

 

[jaus tail]

Sorry I'm not getting it.
I think it can be
Energy store = energy released.
When energy is being stored(load) then input(current entering) is positive terminal. When energy is being released(source) then output(current leaving) is considered positive terminal (kinda like KVL convention)
Thus: (Vs - Vo)Ton = Vo(Toff)

But why V times T and why not V²? Energy is proportional to Voltage square divide by resistance times time.

 

[Baarken]

So in steady state, the average inductor voltage is zero. Which means that the sum of the red area + the blue area is zero i.e. $$V_L = \frac{1}{T_s}\int_0^{T_s}v_L(t)dt = 0 $$
Solving the integral we get, which is easy if you look at the figure below:
$$\underbrace{(V_s-V_o)DT_s}_{\text{red area}}+\underbrace{(-V_0)(1-D)T_s}_{\text{blue area}} = 0$$

Then solving as you did in post #1 yields eq. 13.4.

So I am not sure why they included the minus sign in eq. 13.3 as the_emi_guy pointed out in post #2, other than causing confusion.
If you don't know why, the average inductor voltage in steady state has to be zero, look here:
https://www.quora.com/Why-do-inductors-follow-a-volt-second-balance-principle

 

[Baarken]

Just a correction to my post #8, second equation, should be: $$\frac{1}{T_s}\left[(V_s-V_o)DT_s + (-V_o)(1-D)T_s\right]$$ and not $$(V_s-V_o)DT_s+ (-V_o)(1-D)T_s$$

 

[jaus tail]

Thanks. Got it.