How Does Acceleration Relate Between Two Blocks in a Frictionless Pulley System?

[judas_priest]

Homework Statement

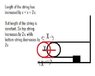
In the system shown, the strings and the pulleys are ideal. There is no friction anywhere in the system. As the system is released, block m1 moves downward.

If the magnitude of the acceleration of block m1 is a, what is the magnitude of the acceleration of block m2?

Homework Equations

The Attempt at a Solution

If mass m1 moves down by x, the pulley attached to m2 moves towards left by 2x, Hence block moves by 2x. Hence, acceleration of block 2 is 2a. Am I right?

I have a problem with constraint equations. If someone could clear it, please.

 

[dreamLord]

No. Think of it this way : if mass m1 moves down by distance x, then all the points on the string attached to it move by distance x. Which means the center of the horizontal pulley also moves to the left by x, not 2x, since after all it is fixed to the string.

 

[judas_priest]

Ya, I realized. How do I relate the acceleration of the two blocks?

 

[dreamLord]

When you displace the horizontal pulley by a distance x to the left, how much excess string would you need for m2 to remain stationary?

 

[judas_priest]

Also, the string it needs to move the distance x, is compensated by block 2 moving to the left by a distance x. Because the other side of the string that run through the pulley is attached to the wall. Therefore, block going down by x, would move the pulley to the left by x. Differentiating twice would give a1 = a2. But that's no the right answer.

 

[judas_priest]

When you displace the horizontal pulley by a distance x to the left, how much excess string would you need for m2 to remain stationary?

How can it remain stationary if the pulley is being displaced to the left? Won't the pulley pull the string, hence pulling the block 2?

 

[dreamLord]

You didn't get my question - if, hypothetically, we were to make the block remain stationary, how much excess string would we need to add to the existing piece?

 

[dreamLord]

EDIT : Double post

 

[judas_priest]

Wouldn't it b x? Because the pulley is moving by x, and therefore it's going to try moving the block 2 by x. If block 2 had an excess x length of string, block 2 wouldn't have to move at all. Am I right?

 

[judas_priest]

What's your approach to this problem? How do you relate a1 to a2?

 

[dreamLord]

Nope. Think of it this way : the top of the pulley moves by a distance x, but the bottom also moves by a distance x. That means both the top portion of the string, and the bottom portion have increased by x, which can't happen as the length of the string is fixed. So the mass moves by 2x to the left.

Basically, your answer is correct, but the method by which you reached it was not.

 

[judas_priest]

Still haven't got it. You mean a1 = 2a2 is correct? Yup, it is. But I got it by manipulation. Haven't understood the problem. I always had a problem with constraints. By the very basics of it.

 

[judas_priest]

If both the top and bottom strings have moved by x, shouldn't it be x1 = x2?

 

[WannabeNewton]

Can the total length of the string(s) change?

 

[judas_priest]

If m2 is extremely large, m1 won't move at all. If m1 is zero, again, the pulley and m2 won't move at all.

 

[haruspex]

If mass m1 moves down by x, the pulley attached to m2 moves towards left by 2x,

In case it's not clear, dreamLord is pointing out that although your answer below is right, the statement above is wrong. To see this, ignore m2 and the string attached to it, and think of the top pulley as just a block. What you may have had in mind is that the top pulley both moves (by x) and rotates.

Hence block moves by 2x. Hence, acceleration of block 2 is 2a. Am I right?

 

[dreamLord]

In this drawing, the figure in red is when the pulley has moved by distance x to the left. Does this help?

 

[judas_priest]

Okay, Thanks! Got it. Haruspex is right. I was considering the pulley to be rotating.

 

[judas_priest]

Also, what would be the tension in the string attached to block 2? Would it be T? I know the tension on the string running from pulley to block 1 is T, because the tension is same in the string throughout. But what about the tension in the string attached to block 2?

Would it be T1₁ = 2T₂? therefore tension on string attached to block 2 would be T₁/2. Correct?

 

[WannabeNewton]

What are the forces on the horizontal pulley? Can there be a net force on the pulley if its massless? Use that to find the relationship between the two tensions.

 

[judas_priest]

Horizontal force on the pulley would be T1₁ = 2T₂, so block 2 would be T1₁/2 = T₂

 

[WannabeNewton]

I think you mean $F_p = T_1 - 2T_2$. And yes if you then use the fact that $F_p = 0$ you will get what you originally stated (I just wanted to make sure you knew why the result followed).

 

[dreamLord]

Yep, that relation is correct for the tensions.

 

[James Faraday]

What I don't get is, given the setup in the original diagram, how can $m_1$ ever move? The right endpoint of the string attached to $m_1$ is fixed to the center of the horizontal pulley and the string around the horizontal pulley is itself anchored to the wall. If $m_1$ tries to accelerate down it will pull on the horizontal pulley but since the string around the horizontal pulley is anchored to the wall, won't the horizontal pulley refuse to budge thus keeping $m_1$ in place?

The only movement I can see happening is that $m_2$ gets pulled forward due to the tension in the string on its end generated by the string attached to the wall resisting the pull of $m_1$ on the horizontal pulley. Thanks!

 

[dreamLord]

The string around the horizontal pulley is itself anchored to the wall.

The horizontal pulley is not anchored to the wall - I think that would happen if we tied a piece of string joining the center of the pulley to the wall.

EDIT : Sorry, you're talking about the string, my bad.

In that case, why should the pulley be stationary? If there is a net force on it, it will move. Where is the constraint?

 

[James Faraday]

Thanks for the response. I'm asking how can the horizontal pulley be moved to the left if the string around it is anchored to the wall? How physically could it possibly be moved to the left by $m_1$ in order so that $m_1$ accelerate down if there is a string looping around the horizontal pulley with one end of the string firmly attached to the wall? Thanks again.

 

[haruspex]

What I don't get is, given the setup in the original diagram, how can $m_1$ ever move? The right endpoint of the string attached to $m_1$ is fixed to the center of the horizontal pulley and the string around the horizontal pulley is itself anchored to the wall. If $m_1$ tries to accelerate down it will pull on the horizontal pulley but since the string around the horizontal pulley is anchored to the wall, won't the horizontal pulley refuse to budge thus keeping $m_1$ in place?

Only one end of the string is anchored. The pulley can move provided it rotates. It'll be like a wheel rolling on the road, except this road is above it.

 

[James Faraday]

Am I correct in imagining that when $m_1$ pulls on the horizontal pulley with enough force, the massless horizontal pulley glides to the left (with zero net force of course) and as it does the bottom part of the string around the horizontal pulley will start rolling over the horizontal pulley because the top end of the string is anchored to the wall so the un-anchored bottom end will move forward, pulling $m_2$ along with it? So in this sense the motion of $m_2$ can only go smoothly until the end of the string it is connected to has caught up with the pulley through the rolling of the string around the pulley? Thanks.

 

[James Faraday]

Basically, could I crudely imagine it like this, with the situation drawn upside down (see attachment)? If so, why do we necessarily need the pulley to rotate (as in attachment)? Why couldn't the pulley simply glide forward and have the string roll over its surface without the pulley having to rotate in order to make it roll? Thanks.

 

[judas_priest]

I have a general question, if a vertical simple pulley had two blocks both of same mass, would the tension in the string be zero?