Allenman
- 58
- 0
This isn't homework or anything, I just want to understand the question better.
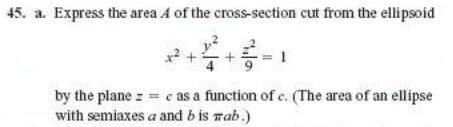
I'm honestly not sure where to go with this. Is this an integral problem? As I understand it I'm finding the area of a slice, not a volume of the whole ellipsoid.
so z = c which = 3...
the problem then becomes:
x^{2} + \frac{y^{2}}{4} = 0
Does the last description mean that the answer is A= (\pi)(1)(2) ?
It doesn't seem like it should be that simple. lol
Homework Statement
The Attempt at a Solution
I'm honestly not sure where to go with this. Is this an integral problem? As I understand it I'm finding the area of a slice, not a volume of the whole ellipsoid.
so z = c which = 3...
the problem then becomes:
x^{2} + \frac{y^{2}}{4} = 0
Does the last description mean that the answer is A= (\pi)(1)(2) ?
It doesn't seem like it should be that simple. lol