paulimerci
- 287
- 47
- Homework Statement
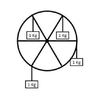
- A 6 spoke wheel with a radius of 2 meters has 4 - 1 Kg masses hanging from the point where the spoke meets the rim as shown. What would be the net torque acting on the wheel?
- Relevant Equations
- Applying Rotational equlibrium, F1d1 + F2d2 = F3d3 + F4d4
F_{1}d_{1} + F_{2}d_{2} = F_{3}d_{3} + F_{4}d_{4}
m_{1} gR cos 60 + m_{2}gR cos 60 = m_{3}gR cos 60 + m_{4}gR sin 90
m1 = m2= m3= m4= m
R1=R2=R3=R4=R
\sigma\tau = sin 90 - cos 60 = 0.5 Nm.
Have I done this right?
m_{1} gR cos 60 + m_{2}gR cos 60 = m_{3}gR cos 60 + m_{4}gR sin 90
m1 = m2= m3= m4= m
R1=R2=R3=R4=R
\sigma\tau = sin 90 - cos 60 = 0.5 Nm.
Have I done this right?