Calculate Distance Dropped to Reach Speed of 10m/s

[gloo]

I am looking at all these speed and acceleration equations on the net but can't find what I need. What I want to calculate is how far do i have to drop water for it to reach a certain speed?

The only equations i see involve asking parameters that I don't know. the only thing i do know is acceleration (9.81m/s square), and initial velocity which is zero. I am looking at final velocity equation Vfinal=Vinitial + a*t

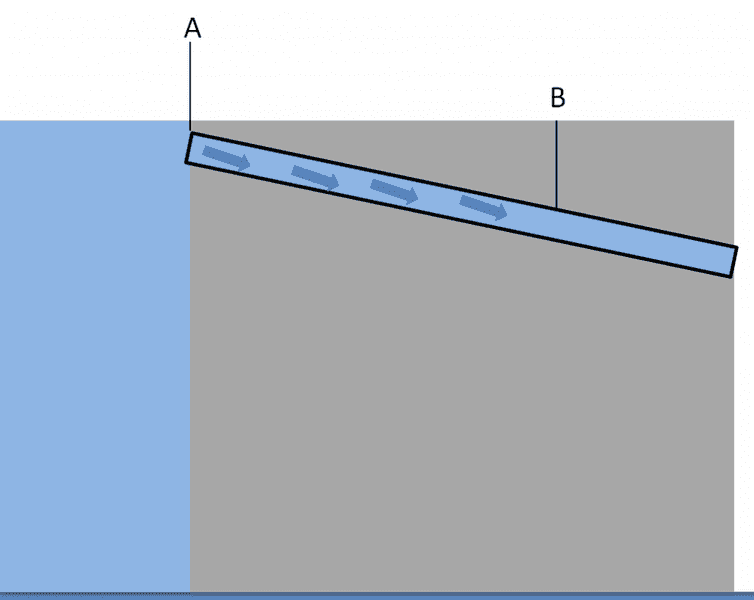
I have attached a diagram of what I am looking at. So at point A, the velocity is 0 (we are holding back water). If I want to achieve say 10meters per second at point B, I assume it has to drop a certain distance vertically??

How do solve for something like that final speed ...If i want to achieve say 10 m/s final velocity?

 

[dipstik]

v_initial is 0 m/s, a=9.81 ms^-2, v_final is 10 m/s. Now solve for t. That will be the time required for the droplet to reach 10 m/s, ignoring drag and terminal velocity.

 

[gloo]

@dipstik. Wait, so it is not a function of how high?? just a matter of time?

 

[gloo]

Vfinal= Vinitial +a*t
10=0 + 9.81 * t
t=1.01 seconds?

 

[dipstik]

to figure out how high you need to plug the time into the position equation.

x=x_0+v_0*t+0.5*a*t^2

but that is assuming free fall... you show a slope... which means you can't use 9.81 directly...

 

[gloo]

Ok, sorry - i gave that equation, so I assumed that was the one to use.

So using your equation :

x=0 +0.5(9.81)(1.01) (1.01)
=5 m

so looking at all of what was just done... if we want to reach 10m/s in 1.01 seconds, we need to drop if from a distance of 5 meters? So the point b depth is 5 meters from the surface of the dam? I am probably wrong...because you say i can't use it directly...So what should i be assuming and what equation do i use if i can't use 9.81m/s^2 directly

 

[sophiecentaur]

In the absence of friction forces, the easiest way to calculate the time to reach a given speed is to equate the gravitational potential energy at the top to the Kinetic energy at the end
For a unit mass gh = v²/2

The actual time taken to reach a given velocity will depend upon the slope but the vertical height will be the same for all (lossless) slopes.
Simples

 

[gloo]

Thanks sophiecentaur...

so g=gravity constant
v=10gh=(10*10)/2
gh=50
h= 50/g
=50/9.81
=5 meters?

actually, I am totally confused now. So we can achieve 10m/s velocity at a certain point (b) with any slope? The more gentler slope would take longer? But a vertical drop would require a higher drop to allow for unfettered acceleration down?

 

[sophiecentaur]

If there is no friction loss, the energy available for accelerating the drops is just mgh, whatever path is taken. Remember, this is totally theoretical and a slope will, in practice, involve more losses than a vertical drop. But Enery Conservation can be applied in a first approximation. The actual details can be very important if you want to take this further.

BTW, in your diagram, the majority of the water in the reservoir will not contribute in any way to the performance. The vertical distance from the water level is what counts and not the drop from point A.

 

[gloo]

Yes I understand that the drop depth is what is important. But I was just trying to see if it was possible to reach 10m/s water speed on only a gentle slope. If the drop was only a meter, is it theoritically possible to make the water go 10m/s if the slope was long enough?

 

[sophiecentaur]

Yes I understand that the drop depth is what is important. But I was just trying to see if it was possible to reach 10m/s water speed on only a gentle slope. If the drop was only a meter, is it theoritically possible to make the water go 10m/s if the slope was long enough?

But you are ignoring what I am telling you and concluding exactly the opposite. The speed depends upon the net loss in height (i.e. lost potential energy) - irrespective of the 'gentleness' of the slope (when there is no friction, of course). If you drop by 1m, however you get there, your final speed will always be the same. (In this universe)
Where else could the energy come from, if not by losing gravitational potential energy?