Calculate Tension of Two Wires: Physics/Precalc

  • Context: High School 
  • Thread starter Thread starter Planetx
  • Start date Start date
  • Tags Tags
    Calculations Tension
Click For Summary
SUMMARY

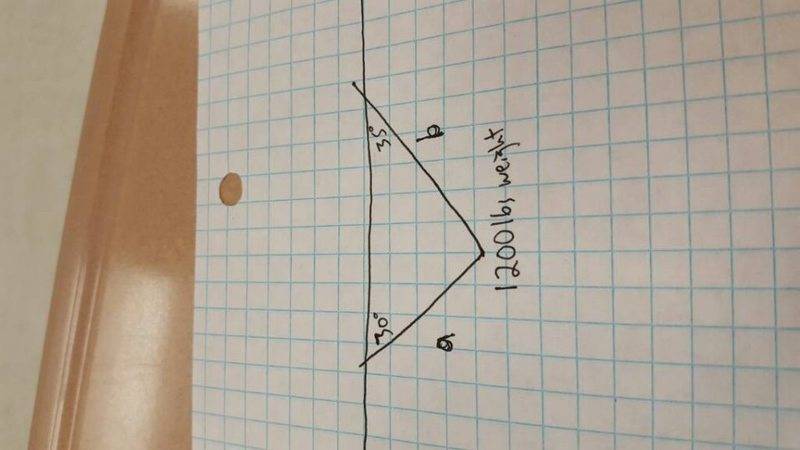
The discussion revolves around calculating the tensions in two wires supporting a 1200 lbs weight at angles A = 35 degrees and B = 30 degrees. The user struggles with the equations, specifically using x = (-ycos35/cos150) and x = (-ycos35/cos180), leading to confusion regarding vector analysis and the application of the angle theorem. The consensus indicates that while the Pythagorean theorem is often applicable, the complexities of tension require a more nuanced understanding of vector components and equilibrium conditions.

PREREQUISITES
  • Understanding of vector components in physics
  • Knowledge of trigonometric functions and their applications
  • Familiarity with the Pythagorean theorem
  • Basic principles of equilibrium in static systems
NEXT STEPS
  • Study vector resolution techniques in physics
  • Learn about static equilibrium and force diagrams
  • Explore the application of trigonometric identities in tension calculations
  • Review examples of tension problems involving multiple angles and weights
USEFUL FOR

High school physics students, educators teaching precalculus concepts, and anyone interested in understanding the principles of tension in static systems.

Planetx
Messages
6
Reaction score
0
I am tasked to find the tensions of two wires by calculating the "magnitude of the vector" in a high school physics/precalc class. I have tried working out the equation in several ways but they all end up in an unsolvable format. So, in reference to the picture, A = 35 degrees, B= 30 degrees and sides a and b symbolize the magnitude or tension on two vectors when holding a 1200 lbs weight from a level position. I am given no other information.
1461943737818.jpg
 
Physics news on Phys.org
I have found that x = (-ycos35/cos150) no? And I tried substituting it into a few equations I worked out. I feel I am in the WAY wrong direction here and common sense is failing me.
 
Planetx said:
I have found that x = (-ycos35/cos180) no? And I tried substituting it into a few equations I worked out. I feel I am in the WAY wrong direction here and common sense is failing me.
I realize this is a simple problem but my application of angle theorem and vector analysis is limited so far.
 
Some people told me pythagorean theorem is that simple but i figured tension would be different from magnitude
 

Similar threads

Undergrad Load on a Horizontal Wire (Zip line)
  • · Replies 1 ·
Replies
1
Views
5K
High School Derivation of Cosine and Sine Method of Vector Sum
  • · Replies 4 ·
Replies
4
Views
2K
Calculate tension and strain of wire
  • · Replies 1 ·
Replies
1
Views
5K
High School Calculate needed dimensions of table - Center of mass, levers etc
  • · Replies 11 ·
Replies
11
Views
3K
High School Force required to stretch training resistance bands
  • · Replies 12 ·
Replies
12
Views
3K
High School A triangle problem: Prove that |AC|+|AB|=|PR|+|PQ| given some constraints
  • · Replies 13 ·
Replies
13
Views
3K
High School Showing/proving a physical relationship
  • · Replies 11 ·
Replies
11
Views
2K
Calculating Tension and Net Force in Suspended Cable System
  • · Replies 3 ·
Replies
3
Views
3K
Vector addition and the force applied to the shaft of the pulley
  • · Replies 4 ·
Replies
4
Views
2K
What is the Tension in Rope Two?
  • · Replies 22 ·
Replies
22
Views
8K