Calculate the electric field in all of space for a non conducting sphere

[cookiemnstr510510]

Homework Statement

A) Use Gauss's Law to derive the electric field in all space for a non-conducting sphere with volumetric charge distribution ρ=ρ₀r³ and radius, R.
B) Repeat when there is a concentric spherical cavity within the non conducting sphere with radius, A.

Homework Equations

∫E⋅dA=Q_enclosed/ε₀
ρ=Q/V (charge density)

The Attempt at a Solution

Im struggling with part B more than A, but since B uses part A's answer (in a way) I will show both my attempts

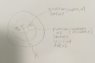
A) I drew a picture (sphere.jpg attached) and will use words to explain what I am doing.
My sphere has radius, R.
My Gaussian Surface has radius, A.
I will be finding dQ of a small spherical piece of the sphere, the radius of this small spherical piece is, r, and has thickness, dr.

First find dQ
we know that ρ=Q/V →dQ=ρdV since ρ=ρ₀r³ and dV=(4πr²)(dr) let's plug those into our dQ:
dQ=(ρ₀r³)(4πr²)(dr)

We can now find our Q_enclosed of gaussian surface.
My below integral's limits go from 0→a (a being the radius of my gaussian surface)
Q_enclosed=∫dQ=∫ (ρ₀r³)(4πr²)(dr)=4πρ₀∫r⁴→once evaluated= (4πρ₀a⁵)/5 (this is our Q_enclosed)
Now we can use gauss's law to find electric field
E(4πa²)=(4πρ₀a⁵)/(5ε₀)
and finally:
E=(ρa³)/(5ε₀)→E(r)=ρr³)/(5ε₀)r(hat)
This is the answer if you are inside the sphere at some distance r<R

Now for outside the sphere:

We can go to the Q_enclosed and just change the limits, instead of integrating from 0→a, we can integrate from 0→R. If we do this our Q_enclosed becomes:

Q_enclosed=(4πρ₀R⁵)/5

My new gaussian surface has radius a'

E(4πa'²)=(4πρ₀R⁵)/(5ε₀)
solving for E:
E=(ρ₀R⁵)/(5a'²ε₀)

Now for part B

Again, new limits for Q_enclosed, the limits now are going from A→a
our new Q_enclosed=[(4πρ₀a⁵)/(5)]-[(4πρ₀A⁵)/(5)]
and our new E=[(ρ₀a³)/(5ε₀)]-[(ρ₀A⁵)/(5a²ε₀)

and outside our Q_enclosed=[(4πρ₀R⁵)/(5)]-[(4πρ₀A⁵)/(5)]
and our new E=[(ρ₀R⁵)/(5a²ε₀)]-[(ρ₀A⁵)/(5a²ε₀)

Hope that was clear enough, please ask for more steps if I am wrong.
thanks!

 

[BvU]

Hello,

Qenclosed=∫dQ=∫ (ρ0r3)(4πr2)(dr)=4πρ0∫r4→once evaluated= (4πρ0a5)/5

How do you do this ?

 

[cookiemnstr510510]

Hello,
How do you do this ?

Ahh, I believe I made a mistake,
It is supposed to evaluate like:
∫ρ₀r³4πr²dr→(2πρ₀a⁶)/3