Calculate the maximum deflection of a simply supported beam
- Thread starter Buzz_Lightyear
- Start date
-
- Tags
- Beam Deflection Maximum
Click For Summary
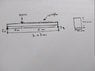
The discussion focuses on calculating the maximum deflection of a simply supported beam with specific parameters: E=220 GN/m², L=7 m, a point load of W=20 kN at 2 m from the left edge, and a uniformly distributed load (udl) of 10 kN/m from x=2 to x=7. The calculations involve using the moment equations and applying Newton's method to solve a cubic equation derived from the deflection formula. The maximum deflection is found to occur at approximately x=3.53 m, yielding a downward displacement of 2.2 mm.
PREREQUISITES- Understanding of beam mechanics and deflection theory
- Familiarity with moment equations and shear force analysis
- Knowledge of Newton's method for solving equations
- Basic proficiency in structural analysis software or programming (e.g., Visual Basic 6)
- Study the application of Macaulay's method for structural problem-solving
- Learn about finite difference methods for approximating derivatives
- Explore the use of iterative methods for solving cubic equations
- Investigate the principles of beam deflection and load distribution in structural engineering
Structural engineers, civil engineering students, and professionals involved in beam analysis and design will benefit from this discussion, particularly those seeking to understand deflection calculations and methods for solving complex equations in structural mechanics.
Similar threads
- · Replies 8 ·
- · Replies 8 ·
- · Replies 1 ·
- · Replies 1 ·