Calculate the natural circular frequency ωn of the system

[Alex Katko]

Homework Statement

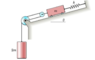
Calculate the natural circular frequency ωn of the system shown in the figure. The mass and friction of the pulleys are negligible. The diagram is attached.

Homework Equations

ωn = (k/m)^1/2

The Attempt at a Solution

I can see the total mass of the system is 3m. So in the equation instead of m, the equivalent mass of the system is 3m. The equivalent k is giving me some difficulties. I know that is has to do with x (the spring deflection) and how it relates to the system.

My thought was that if the spring moves x meters down the slope, then the larger mass (2m) will move only 1/2*x meters down. Thus, my solution was ωn = [(k/2)/(3m)]^1/2 or ωn = (k/6m)^1/2

The correct answer is ωn = 1/3*(k/m)^1/2

 

[haruspex]

So in the equation instead of m, the equivalent mass of the system is 3m.

Are you sure? Do they move with equal accelerations?

if the spring moves x meters down the slope, then the larger mass (2m) will move only 1/2*x meters down.

Check that.

The correct answer is ωn = 1/3*(k/m)1/2

I don't think that is right either.

 

[kuruman]

Your thought is correct, but your conclusion does not follow. Instead of divining the answer, do it formally. Draw FBDs for each mass and construct an equation of the form $ma = (some factor)kx+(some~constant)$, where $a$ is the acceleration of the mass on the incline and $x$ is the displacement of the spring from equilibrium. Then the frequency is given by $\omega^2=\frac{(some~factor)k}{m}$.

On edit: As @haruspex commented, if the hanging mass moves by half the distance as the mass on the incline in the same time, then the two accelerations cannot be the same.

 

[haruspex]

Your thought is correct, but your conclusion does not follow. Instead of divining the answer, do it formally. Draw FBDs for each mass and construct an equation of the form $ma = (some factor)kx+(some~constant)$, where $a$ is the acceleration of the mass on the incline and $x$ is the displacement of the spring from equilibrium. Then the frequency is given by $\omega^2=\frac{(some~factor)k}{m}$.

On edit: As @haruspex commented, if the hanging mass moves by half the distance as the mass on the incline in the same time, then the two accelerations cannot be the same.

Do you agree the given answer is also wrong?

 

[kuruman]

o you agree the given answer is also wrong?

Yes, the "correct" answer as posted by OP is not what I got, but I can see how a typo may have been introduced ...

 

[Alex Katko]

Yes, the "correct" answer as posted by OP is not what I got, but I can see how a typo may have been introduced ...

There was no typo, the answer is 1/3*(k/m)^1/2

 

[kuruman]

There was no typo, the answer is 1/3*(k/m)^1/2

If you posted the "correct" answer exactly as was given to you, then a possible typo occurred when that answer was written down. To figure out the frequency of oscillations you can (a) draw a free body diagram for each mass, relate the accelerations according to your thought and write an equation for the acceleration of the mass on the incline. Compare that with the acceleration of a horizontal spring-mass system and extract the frequency of oscillations; (b) figure out how angle $\theta$ affects the frequency of oscillations, set $\theta = 90^o$ and compare the frequency that you get with the frequency of a vertical spring-mass system.

 

[gneill]

My thought was that if the spring moves x meters down the slope, then the larger mass (2m) will move only 1/2*x meters down.

You may want to revisit that thought.

 

[Alex Katko]

Are you sure? Do they move with equal accelerations?

Check that.

I don't think that is right either.

I'm pretty bad at understanding pully not sure why. The accelerations should not be equal. I would say the acceleration of the 2m mass is twice the acceleration of the 1m mass

 

[Alex Katko]

If you posted the "correct" answer exactly as was given to you, then a possible typo occurred when that answer was written down. To figure out the frequency of oscillations you can (a) draw a free body diagram for each mass, relate the accelerations according to your thought and write an equation for the acceleration of the mass on the incline. Compare that with the acceleration of a horizontal spring-mass system and extract the frequency of oscillations; (b) figure out how angle $\theta$ affects the frequency of oscillations, set $\theta = 90^o$ and compare the frequency that you get with the frequency of a vertical spring-mass system.

Okay here is what I have now. Since the spring starts off stretched a bit, I should do a static force balance first, and find the tension in the string and the static displacement of the spring. Doing this I end up with two equations.
1. From the 2m mass, T - 2mg = 0
2. From the 1m mass, kx - 2T - mgsin(θ) = 0 where the direction is along the slope of the ramp.

I should then do the dynamic case, where the new tension is T', which changes over time. Once again i get two equations.
3. T' - 2mg = 4ma
4. kx' - 2T'-mgsin(θ) = ma

The first equation has 4ma the mass is 2m and the acceleration should be twice that of the smaller mass, so multiply by a factor of 2.

Assuming this is correct (which isn't too likely) my next confusion is what is x'? I think x' should be x (solved from the first 2 equations) minus some other distance based on how far the masses move.

 

[haruspex]

Okay here is what I have now. Since the spring starts off stretched a bit, I should do a static force balance first, and find the tension in the string and the static displacement of the spring. Doing this I end up with two equations.
1. From the 2m mass, T - 2mg = 0
2. From the 1m mass, kx - 2T - mgsin(θ) = 0 where the direction is along the slope of the ramp.

I should then do the dynamic case, where the new tension is T', which changes over time. Once again i get two equations.
3. T' - 2mg = 4ma
4. kx' - 2T'-mgsin(θ) = ma

The first equation has 4ma the mass is 2m and the acceleration should be twice that of the smaller mass, so multiply by a factor of 2.

Assuming this is correct (which isn't too likely) my next confusion is what is x'? I think x' should be x (solved from the first 2 equations) minus some other distance based on how far the masses move.

Yes, it will help to express everything in terms of the independent variable (y, say) = x'-x.
Your equations look good.