rdemyan
- 67
- 4
Thread moved from the technical forums to the schoolwork forums.
- Homework Statement
- center of mass problem
- Relevant Equations
- Provided in post
TL;DR Summary: Calculate the speed and angle of the center of mass before a collision
I want to calculate the speed and angle of the center of mass (CM) before a collision for a two dimensional problem.
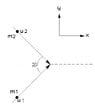
The direction of the CM will be inferred from a drawing or from the calculated angle. So as shown in the drawing - two particles collide at an angle of ##2\beta##. The x-axis exactly bisects this collision angle so the angle of interest is ##\beta##. The masses of the particles are ##m_1,m_2## and the velocities are ##u_1,u_2##.
So, the way I see calculating the speed of the CM is to calculate the momentum in the x direction and y direction. Then use the pythagorean theorem to get the momentum along the angle of the CM and divide by the sum of the masses to get the speed. So,
$$u_{cm} = \frac{\sqrt{(m_1u_1cos\beta + m_2u_2cos\beta)^2 +(m_1u_1sin\beta - m_2u_2sin\beta)^2}}{m_1+m_2}$$
And the angle of the CM relative to the x axis is given by
$$ \alpha = tan^{-1}(\frac{m_1u_1\sin\beta - m_2u_2\sin\beta}{m_1u_1\cos\beta + m_2u_2\cos\beta})$$
Am I looking at this correctly and are the equations correct for this particular situation?
View attachment 359396
I want to calculate the speed and angle of the center of mass (CM) before a collision for a two dimensional problem.
The direction of the CM will be inferred from a drawing or from the calculated angle. So as shown in the drawing - two particles collide at an angle of ##2\beta##. The x-axis exactly bisects this collision angle so the angle of interest is ##\beta##. The masses of the particles are ##m_1,m_2## and the velocities are ##u_1,u_2##.
So, the way I see calculating the speed of the CM is to calculate the momentum in the x direction and y direction. Then use the pythagorean theorem to get the momentum along the angle of the CM and divide by the sum of the masses to get the speed. So,
$$u_{cm} = \frac{\sqrt{(m_1u_1cos\beta + m_2u_2cos\beta)^2 +(m_1u_1sin\beta - m_2u_2sin\beta)^2}}{m_1+m_2}$$
And the angle of the CM relative to the x axis is given by
$$ \alpha = tan^{-1}(\frac{m_1u_1\sin\beta - m_2u_2\sin\beta}{m_1u_1\cos\beta + m_2u_2\cos\beta})$$
Am I looking at this correctly and are the equations correct for this particular situation?
View attachment 359396
Attachments
Last edited: