Calculating Area of a Wedge Cut from a Cylinder

[nobahar]

Hello!
I've seen volume calculations involving cutting a wedge from a cylinder where the wedge cuts down to the centre of the circle (i.e. the length of the straight edge will be the diameter of the cylinder).
I was looking for hints on working out the area of a wedge cut from a cylinder where the wedge goes straight across from one side of the cylinder to the other; if that makes sense.
If not, here's my poor attempt at a drawing to illustrate:

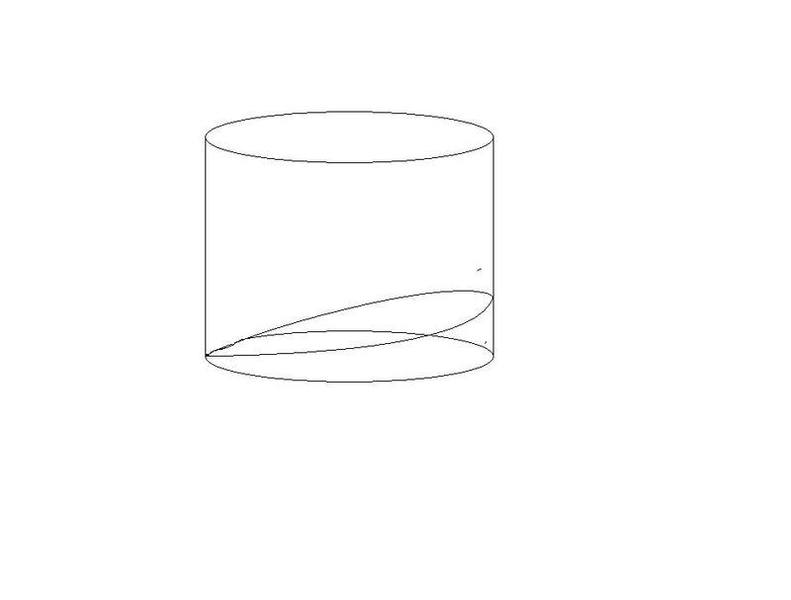
Anyone know any websites or any hints? As I say, the only ones I found pertain to wedges where, I believe, the angle of the cut remains constant (where the cut is from the centre), I believe the angle changes in my example.
Thanks in advance.

 

[lanedance]

i'm not too sure what you mean exactly - is the cut a plane... what angle are you talking about & how/why does it vary?

If it is cut by a plane, it should be easy to come up with the volume from symmetry & the volume of a cylinder. Otherwise you'll probably need to look at setting up a volume integral.

 

[LCKurtz]

I don't see why the angle between the slanted surface and the bottom would change. Suppose your cylinder was just tall enough to fit the wedge. Wouldn't the volume be just half of that cylinder?

Disclaimer: I haven't worked it out; that's just my best guess.

Edit: I have now and it is.

 

[nobahar]

I don't see why the angle between the slanted surface and the bottom would change.

I was thinking of integrating by adding up the area of lots of triangles; as you would in example 4 on this page:

http://tutorial.math.lamar.edu/Classes/CalcI/MoreVolume.aspx

In my example, I now think only one would be a triangle, the very centre one, the others wouldn't be.

Suppose your cylinder was just tall enough to fit the wedge. Wouldn't the volume be just half of that cylinder?

Argggghhhh! That's so simple I completely overlooked it! I was thinking it would be long and 'difficult'. Although it (now you've pointed it out) seems obvious, is there another way I can prove this is so? That it is half the cyclinder up to the peak of the wedge?
Many thanks to both of you for the responses.

 

[LCKurtz]

Argggghhhh! That's so simple I completely overlooked it! I was thinking it would be long and 'difficult'. Although it (now you've pointed it out) seems obvious, is there another way I can prove this is so? That it is half the cyclinder up to the peak of the wedge?
Many thanks to both of you for the responses.

You can do it as an integral too. If the cylinder is x²+y² = a², and the plane is inclined at an angle α in the zy trace, then the equation of the plane is

z = (y + a) tan(α) [Why?]

so the volume of the wedge would be

\int\int_D (y + a)\tan(\alpha)\ dydx

where the integral is over the circular domain D. You will want to use polar coordinates.

 

[Jerbearrrrrr]

To prove it, you have to construct some symmetry that maps the unwanted half exactly onto the wanted half I guess.
(The symmetry itself is obvious...but might be a bit yucky to prove)
[edit] by yucky, I mean you might have to explicitly use coordinates.

 

[nobahar]

z = (y + a) tan(α) [Why?]

Why is this the equation of the plane?
Sorry, I'm fairly new to plane equations, I've started to read about it, but nothing that looks like the above equation. (My maths is largely self-taught).
Again, many thanks.

 

[LCKurtz]

Why is this the equation of the plane?
Sorry, I'm fairly new to plane equations, I've started to read about it, but nothing that looks like the above equation. (My maths is largely self-taught).
Again, many thanks.

Look at just the intersection of the plane with the zy plane (the zy cross-section in your picture). That intersection is just a straight line. It intersects the y-axis at y = -a. α is just the angle of inclination of the line and tan(α) is the slope. So you know a point and the slope and can write the equation of that line. Since the plane is parallel to the x axis, the same equation represents the equation of the plane. The x variable being missing makes the surface parallel to the x axis.

Also note that you can write the slope tan(α) in terms of a and the height h of the shortened cylinder.

 

[nobahar]

Many thanks LCKurtz. Circular domains and using polar co-ordinates in integration is something I haven't yet looked in to. But I will refer back to this thread when I do!