Calculating distance (from magnet) to an arbitrary point in 3D space

[egoodchild]

TL;DR

Looking to learn how to calculate the distance from the center of a magnetic dipole to an arbitrary point in 3D space assuming we know the B-field at that arbitrary point as well as the characteristics of the dipole in question.

So I'm looking for some advice on a problem that I am trying to solve for a project. I'm an engineer but my background in vector mathematics is very minimal so I'm looking for some assistance.

Lets assume we have a permanent magnet. We know the characteristics of this magnet, such as it's dimensions and residual flux density, etc. Now let's say we pick some arbitrary point away from this magnet in 3D space and we define the distance from that point to the center of the magnet as 'r'. Additionally we measure the B-field at this arbitrary point and know the field strength in all 3 dimensions.

I would like to be able to calculate the distance 'r' from the center of magnet to the arbitrary point in meters.

Now from what I have gathered so far I think the way to do this is by using the equation for a magnetic dipole:

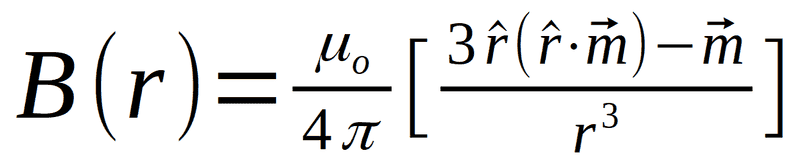
Above image from K&J Magnetics

Where m is:

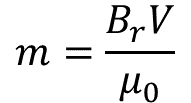
B is known, m is known and we are looking to calculate 'r'.

Now where I get a bit lost is finding the reciprocal of this equation in vector form. As mentioned my end goal is an equation that has an input of B and output of r.

Any help on how to derive this or a resource to take a look at to help would be great.

Thanks in advance!

 

[andrewkirk]

You don't need to get a reciprocal in vector form. Just take the magnitude of both sides. Then you have
$$\|B\| =B = \frac{\mu_0}{4\pi} \frac{\|3\hat r(\hat r\cdot \vec m) - \vec m\|}{r^3}
=\frac{\mu_0}{4\pi} \frac{\|(3 m \cos\theta)\hat r - \vec m\|}{r^3}
$$
where $\theta$ is the angle between $\hat r$ (the unit direction vector pointing at the point you're interested in) and $\vec m$.

The symbols $\|...\|$ indicate taking the magnitude of a vector.

This is a scalar equation that you can solve for $r$ in the usual way. The only vector bit is working out the vector $(3 m \cos\theta)\hat r - \vec m$ and getting its magnitude. You can do that with a diagram, or by calculation if you have the components.

 

[egoodchild]

Thanks so much for the reply! Solving a scaler equation in the usual way is where I'm stuck. I don't know how to go about solving a scaler equation. This level of math is not by strongest subject.

 

[nasu]

But you may have the same magnitude of B at different distances. The relationship does not have to be one-to-one. The field does not have spherical symmetry, does it?

 

[egoodchild]

You are correct, there are going to be multiple locations where B (and r) will have the same absolute magnitude. For my application this is fine, I'm only interested in knowing the total distance my arbitrary point is away from center of the magnet.

 

[nasu]

No, B will have the same magnitude for different values of r, not for the same r. So you cannot tell just from the magnitude of B what is the distance. There is no unique answer. It's not just the positon being undetermined but the distance itself. Look at a map of lines of equal B for a magnet. You will see that they are not circles (spheres).

 

[egoodchild]

For my application, size/shape of magnet my B-field is mostly spherical. This can be seen in a magnetics simulation:

The contours of the field do change direction as you move around a circle from the origin at a fixed radius, however the absolute value of B will be mostly constant. This can be observed above as the color contour being circular in nature.

So from a basic perspective, I know what I'm trying to achieve is possible (although be it only in constrained conditions).