Calculating Electric Field Magnitude and Direction

[willydavidjr]

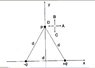
Two point charges of magnitude +q and -q are placed on x-axis separated by distance d, as shown in the figure I provided (You can also look at the website I created). The point P together with the points where the two charges are placed forms an equilateral triangle. What are the direction and strength of the electric field at the point P? Let the constant of proportionality in Coulomb's Law be k.


My idea:
a.) For the direction, we can see that if use to calculate the electic field, point P will be positive and in that case, the Resultant force for y-axis will be zero because it cancels out. So the x-axis will rule in this point so it will probably points in the direction D. Am i correct?

b.)Also calculating the electric field using point P as positive charge, it will also cancel out and the resulting magnitude will be (From equation: E=F/q) E= 2kq/d. Am I also correct?


This is the website: www.geocities.com/willydavidjr/electricfield.html

 

[Lyuokdea]

a.) You are correct, the electric field points in the direction D as depicted in the graph, that is, it points in the -x direction.

b.) Not quite. Remember that although the total electric field for each particle has a magnitude (total strength) of kq/d, the direction that it is pointing in is not the same as the direction of both particles together.

As you said before, some of the force (and by extension the electric field) will cancel out. That is the correct way to think about this problem. You need to find which what part of the electric field for each particle points in the -x direction, and what part points in the y direction.

I find it is helpful to draw a picture of the problem, and physically draw the way the field points for each individual particle at point p, then break down the line you draw into an x and y part in order to find the resultant field.

Hope this helps, if you need any clarification feel free to ask.

~Lyuokdea

 

[willydavidjr]

The resultant field for the y-axis will cancel out because the 1st force
is on the positive y-axis and the 2nd force is on the negative y-axis. But on the other hand, the resultant force for the x-axis is both on the negative side so I will just add them. That's why I get E=2kq/d. Am i right?

 

[dimensionless]

I don't think the equation you're using to calculate the electric field is correct.

 

[Kaworito]

Here's my reasoning.
Each individual field is the same on the point P E1=E2=Kq/d^2

But I know the Y components of each of the fields cancel out. The resultant field is the addition of the X components of each field (which are the same).
E=2E1*cos(w)
where w is the angle between the horizontal and the diagonals of the triangle.
We can see that cos(w) = (d/2)/d = 1/2 ,
so E=E1= (Kq)/d^2

I think this makes kinda sense... what do you guys think? ^^U

 

[borisleprof]

The calculations for the intensity of the electric field made by Kaworito are ok.And the field points in the -x direction.

If you imagine a test charge Q(>0] at point P,
this test charge will be repelled by the (+q) charge with a force that has an intensity of KqQ/d^2; this force is in +q -> Q direction.
With th same intensity, KqQ/d^2, the test charge Q is attracted toward the charge -q.

By symetry of the figure, those forces will cancel in the y direction.

In the -x direction each force collaborate with the value KqQ/d^2 * cos60˚= (1/2)*KqQ/d^2

The resultant force is in the -x direction and is equal to KqQ/d^2.

The electric field will point in the same direction with the intensity equal to Kq/d^2.

 

[skanda9051]

What is the direction of electric field if both have same charge