Calculating Force for Garden Storage Box Lid: A Newton/Kilogram Question

[Chessman]

Hi All
New to this forum.
I just am no expert in this field and I'm a little bamboozled at this problem I have.

I am in the process of constructing a storage box in the garden. Mainly for a couple of bicycles.
I want to put a hinged lid on it. The lid will be constructed from timber and corrugated sheet metal. When getting the bikes in and out of the (open fronted) box, I would like the lid to stay where it's put when I lift it, without the use of wooden props etc.
This points to the used of gas struts. The kind of things that hold the tailgate in the air on a car.
I can buy these on Ebay, but they come in different levels of force, anywhere between 30N and say 170N. I do not entirely understand Newtons vs Kilograms and need to buy the models best suited to the eventual weight of the lid.
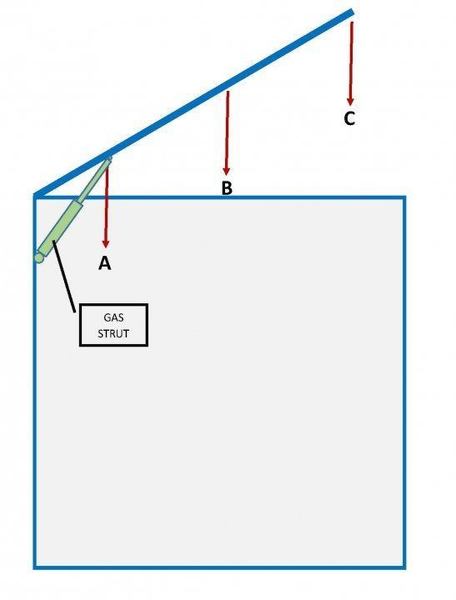
Using the diagram as a guide...Lets say the lid once constructed weighs 25kg. Then I fix it to the box.
The gas struts (I'll use one each end) are not very long, maybe 400mm at most, will be fixed close to the hinge of the lid, between the rear of the box and the lid itself.
The thing that is bamboozling me is I figure that the weight (or Newtons) at the front of the lid is going to vastly increase the nearer you get to the hinges. So: N at point A will be a lot greater than N at point C.
How the heck do I work out which pressure of gas strut I need? My brain is in meltdown, lol.
It has to be enough to hold the lid open, but easy enough to close also.
Also, I'm guessing that the angle the strut is set at is also going to have an impact in performance...would it be better set vertically?
Many thanks in advance.

 

[Tazerfish]

Ok first of all i am going to answer the easiest question.
Here on Earth the gravitational force on one kilogramm is 9.81 Newton.(roughly 10)
So you have to push up on that 25 kilogramm lid with a force of 250 Newtons for it to stay up.

The problem however is more complex.
For the Lid stay up you will need more than its own weight in force.
Why ?
Well you can think of this as forces acting on a lever.
There is on one hand the weight pushing down on the lid in the center.
And on the other hand the gas strut pushing up.

How much force you need exactly is very dependant on how the gas struts are positioned.
If i had to take a guess i would say you need quite a lot more force than the weight of lid.
Maybe like two or three of the 170 Newton gas struts.(that could be overkill)
For a more exact estimate you'd have to post some more details on the size of the gas struts and the lid.

 

[Tazerfish]

Ok now that i think of it my rouugh estimate is pretty much worthless.
You'd really need more information.

 

[Chessman]

Thanks so much for your answer.
I have been out for dinner and only just had a chance to reply.
The lid isn't constructed yet so it's all hypothetical at the moment. I appreciate that the location/size/angle of the gas strut is critical for calculations of force. Other than the size of the strut the other two factors I can adjust ad hoc.
I will be using a strut at each end of the lid though.
I will update once the storage box is constructed (minus struts).
In hindsight I was jumping the gun with this question, but I think too far ahead sometimes, lol.
Thanks again.

 

[CWatters]

The gas struts (I'll use one each end) are not very long, maybe 400mm at most,

At the very least you will need to know the length of the strut in the compressed and extended state.

Then you can work out the geometry and then the gas pressure.

 

[Tazerfish]

I just had a weird idea(which might be stupid):
You could just buy gas struts that would be slightly too weak
and then use a sort of counterweight on the other side of the lid.
(It would help if you made the lid too big for the box so you don't have to build a separate contraption for the counterweight.)
You could then finely adjust the position and mass of the counterweight until it works like you want it to.
The red arrows in the diagram are the forces.

 

[Chessman]

This would be feasible if the box wasn't going up against a wall.
I am going to have a look at the gas struts available.
I had an idea though...
If I marked a point on the lid where the gas strut is likely to anchor, let's say for sake of argument 400mm in from the hinges (approx point A on my original diagram) then place a set of digital bathroom scales directly beneath this point and prop the lid at said marked point, with the base of the prop on the scales, I should have a pretty good idea of the force (at least in kg) being exerted. Once this can be converted to Newtons, and divided by 2, I should have a pretty close guide on the N force needed at each strut.
Just an idea.
I think the struts would need to be set at 90 degrees to the lid, or maybe vertical, and not as In my original diagram, as this would (I think) increase the load substantially.

 

[CWatters]

As drawn the strut provides max force when the lid is down and very little when it's up - especially if fully up is 90 degrees.

If you point the strut backwards it reduces the force when down and increases it as the lid is raised.

 

[Tazerfish]

As drawn the strut provides max force when the lid is down and very little when it's up - especially if fully up is 90 degrees.

If you point the strut backwards it reduces the force when down and increases it as the lid is raised.

Are you really talkting about force here ? I looked up some data on gas springs and it seems the force doesn't really change much with extension.
So i assume you are talking about torque. Right ?

 

[CWatters]

Yes, I should have been clearer. As drawn when the lid is vertical the gas strut is unable to keep it in that position (eg if there is any wind).

This is due to the geometry. I didn't mean to imply the force provided by the gas strut changed.

 

[Nidum]

Nicely done

 

[CWatters]

This is how I was thinking it should be done. This way gas strut provides no force when the lid is down and max force when the lid is up (even if the force provided by the gas strut on it's own is constant). The lid will stay in either position. It won't tend to open on it's own or shut if there is a wind blowing. Might be harder to get the dimensions of the strut right?

 

[Tazerfish]

This is how I was thinking it should be done. This way gas strut provides no force when the lid is down and max force when the lid is up (even if the force provided by the gas strut on it's own is constant). The lid will stay in either position. It won't tend to open on it's own or shut if there is a wind blowing. Might be harder to get the dimensions of the strut right?

View attachment 101703

That is a nice idea.
This way you might even need significantly less force than the weight of the lid.

 

[Complex Root]

You should check out some of the specialized gas spring shops online and their calculation tools. These design your gas spring for you, producing the extended/closed lengths, force rating, and mounting positions, and some have simulators showing the hand force needed to operate the lid throughout its range, plus instruction videos.

The correct gas spring will allow the lid to be lifted from closed with a few 'kilos' of force (note the difference between weight (which is a force) (N) and mass (kg) :- W = mg, g = 9.8), and as the lid is lifted upward this force will diminish to zero at some intermediate angle $\theta_{0}$, eg typically about $30\!-\!45^\circ$, then from there on a downward force of a few kilos is needed to hold the lid back. Above $\theta_{0}$ the lid will move upwards by itself, below $\theta_{0}$ it will close by itself, and at $\theta_{0}$ (and slightly to either side due to friction) it will remain stationary by itself - as can be seen with a typical car boot lid.

For the basic principle of Physics involved see the diagram below showing the various forces acting on the lid. We need to relate the hand force $F_{l}$ on the lid at equilibrium to the gas spring force $F_{s}$. Any less force than $F_{l}$ the lid will then start to move, and any more and it will move in the opposite direction. This is governed by the basic equation for a `rigid body' rotating about a fixed axis, $\tau = I\alpha$. The same principle applies to a lever, or a scale balance with two unequal arm lengths.

$\tau$ is the torque or `moment of force', ie the tendency of the force to cause rotation. We add up the total $\tau$ due to all the forces acting on the lid, ie gravity, hand force, and spring force. To obtain the torque we multiply the force by the perpendicular distance to the axis (this distance is called the `moment (or lever) arm' of the force - eg for spring force $F_{s}$ it is the distance $h$ in the diagram).

In the case of the gravitational force, ie the weight, it is distributed over the entire lid, however it is equivalent to the total weight acting at the center of mass - so the moment arm is $\frac{1}{2}D \cos \theta$.

If we take positive torque to be anti-clockwise, and assume two identical springs the equilibrium condition is then
$$\tau = 2F_{s}h + F_{l}D - \frac{1}{2}(D \cos \theta) F_{g} = 0$$ The trickiest term in this equation is the moment arm $h$, but with some trig (a good maths exercise!) it can be shown to depend on $\theta$ as $$h = c (1 - \cos^{2} \psi)^{1/2} - b \cos \psi,$$ where
$$\cos \psi = (c - a \cos \theta)(a^{2} + b^{2} + c^{2} + 2a(b \sin \theta - c \cos \theta))^{-1/2}.$$ This could then be entered in a graph plotting program to allow the hand force $F_{l}$ to be plotted against $\theta$, for a given spring force $F_{s}$

We could get an initial ball park figure for $F_{s}$ by finding which value requires a few kilos lifting force when lid is closed (ie $\theta = 0$) eg suppose a 50kg lid with D = 0.75m, a = 0.4m, b = 0.09m, c = 0.1m, and a 5kg lifting force, then $F_{s}$ = 639N. Then with that $F_{s}$ you could plot the graph and see the variation of $F_{l}$ throughout the full range of $\theta$. Alternatively you could just store the formula in your calculator and compute $F_{l}$ for various angles $\theta$ eg steps of $10^\circ$, eg for the above example at $\theta = 80^\circ$ we get $F_{l}$ = -10.8kg, ie a 10.8kg downward force to hold the lid. In practice the spring's maximum extension will limit $\theta$ to a certain maximum value.

The online calculators are a good deal more sophisticated than the above model as they also take into account the force variations of the gas spring due to (i) increase of gas pressure inside spring when compressed due to rod entering cylinder and reducing the gas volume (eg a typical spring might vary from 300N-400N due to this), and (ii) the substantial friction force of the tight-fitting seal which causes greater spring force during compression than during extension.

To get an idea of a lifting force in kg you can stand on a bathroom scale whilst holding some everyday objects and note the difference from your normal weight, eg a guitar would be about 3kg, a heavy toolbox about 12kg.

 

[Geordielad]

Hi I have a very similar problem to this just different geometry and I am trying to follow your example above so that I can determine the $F_s$ force for my arrangement. Could you please explain what $\cos\psi$ refers to as it is not shown in the diagram.
Thanks

 

[berkeman]

Hi I have a very similar problem to this just different geometry and I am trying to follow your example above so that I can determine the $F_s$ force for my arrangement. Could you please explain what $\cos\psi$ refers to as it is not shown in the diagram.
Thanks

That post above by @Complex Root is from 7 years ago, and checking their Profile page they have not been here since 2021. But perhaps I can help:

It looks like they just defined $\cos\psi$ in terms of $\theta$ and $a$, $b$ and $c$. Do you see where they did that right after using it in an equation? Does that help?

 

[Geordielad]

Thanks, I do see the formula and I understand angle$\theta$ but I do not understand what angle$psi$ is. I think I must have $\cos\psi$ to figure out what "h" is and I need "h" to figure out what $F_s$ is, which is my ultimate goal. I have inserted my figures to $\cos\psi$ and "h" it is just I am not sure what $\cos\psi$ is.

 

[CWatters]

I don't think Cos(psi) is necessarily a real angle you can point to on the drawing. I might be wrong but I think he introduced Cos(psi) just to simplify the equation for h.

He defined Cos(psi) right below so you could substitute and eliminate Cos(psi) from the equation for h to produce a new equation that only features cos(theta).

 

[Geordielad]

Thanks.

 

[Complex Root]

The angle $\psi$ is the angle the gas spring makes with the horizontal, on the left hand side, ie the angle $S \widehat{P} Q$. The equilibrium formula relates $F_s, F_l, D, F_g$ in terms of the parameters $a, b, c, \theta$, and $\psi$. However it might be more convenient to eliminate $\psi$ to see how the relationship varies with just $a, b, c$ and $\theta$, hence the above relation expressing $\cos \psi$ in terms of the latter four.

To see how the formula for $\cos \psi$ arises we need to consider the triangles $SPQ$ and $SQO$, and the four-sided figure of their union, and we need two additional parameters $d$ and $\phi$, as shown in Figs 1, 2, and 3 below.

From Fig 1, we have :
\begin{align}
L \cos(180 - \psi) & = a \cos \theta - c \nonumber \\
\Rightarrow \cos \psi & = (c - a \cos \theta) L^{-1} \hspace{4em} (1) \nonumber
\end{align}

From the cosine rule applied to triangle $SPQ$ in Fig 2 :
$$
L^2 = d^2 + c^2 - 2 d c \cos \phi \hspace{8em} (2)
$$

To express $d$ and $\phi$ in equation (2) in terms of $a, b, \theta$ we can use triangle $SQO$ in Fig 3. Applying the cosine rule gives :
\begin{align}
d^2 & = a^2 + b^2 - 2 a b \cos(\theta + 90) \nonumber \\
& = a^2 + b^2 + 2 a b \sin \theta \hspace{8em} (3) \nonumber
\end{align}
and applying the sine rule gives :
\begin{align}
\frac{\sin(\theta + 90)}{d} & = \frac{\sin(90 - \phi)}{a} \nonumber \\
\Rightarrow \frac{\cos \theta}{d} & = \frac{\cos \phi}{a} \nonumber \\
\Rightarrow d \cos \phi & = a \cos \theta \hspace{8em} (4) \nonumber
\end{align}
Then combining the equations (2), (3), and (4) we have :
\begin{align}
L^2 & = a^2 + b^2 + 2 a b \sin \theta + c^2 - 2 a c \cos \theta \nonumber \\
\Rightarrow L^{-1} & = (a^2 + b^2 + c^2 + 2 a (b \sin \theta - c \cos \theta) )^{-1/2} \nonumber
\end{align}
giving the required formula for $\cos \psi$ from equation (1).

To see how the formula $h = c (1 - \cos^{2} \psi)^{1/2} - b \cos \psi$ arises we require to show the perpendicular distance from the point $O$ to the line $PQ$ is given by $h = c \sin \psi - b \cos \psi$. A general formula for computing the perpendicular distance of a point $A$ from a line $L$ in 3D space is : $$h = \mathbf{r . v - r_0 . v}$$ where $\mathbf{v}$ is a unit normal vector to $L$ pointing towards $P$, $\mathbf{r}$ is the position vector of point $A$, and $\mathbf{r_0}$ is the position vector of any point on $L$. Applying this to the present situation we have, $\mathbf{r_0} = (c, -b)$, $\mathbf{r} = \mathbf{0}$, and from Fig 1 or 2, $\mathbf{v} = -\cos (\psi-90)\;\mathbf{i} + \sin (\psi-90)\;\mathbf{j} = (-\sin \psi)\;\mathbf{i} + (-\cos \psi)\;\mathbf{j}$, giving $h = -\mathbf{r_0} . \mathbf{v} = c \sin \psi - b \cos \psi$, as required.

In the original post there was one torque force on the lid that was neglected in the equilibrium equation, namely a force perpendicular to the gas spring at $Q$, acting between the lid and the gas spring. This force keeps the gas spring itself in equilibrium about the point $P$ and can be neglected if the weight of the gas spring is negligible compared with the other forces present. The torque this force produces on the lid about $P$ is equal to the torque on the gas spring from its own weight about the point $P$. The longitudinal force component $F_s$ is the force the gas spring is rated for.

There was an error in the original post in the calculation of the lid force required for equilibrium at $\theta = 80^\circ$ for a $639N$ spring. The correct values were : $\cos \phi = 0.0629$, $\sin \phi = 0.9980$, $h = 0.0941$, and $F_l/g = -12.0$kg.