Calculating Input impedance of a CC amplifier

[brainbaby]

TL;DR

comparing input impedance calculated manually and via ltspice

Hi friends,

Here is a CC amplifier
The objective is to calculate its input impedance.
Two ways are employed.
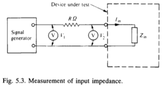
*calculating input impedance using series resistor method (manual method) (refer first two attachment)
V1 = 1mV = 0.001 V
V2 = 656.4129mV = 0.6564129 V
R = 1K
Iin = 343.83207µA = 0.0003438 A
Zin = R / V1/V2 -1
Zin = 1001.5257 Ohm (input impedance)

The value on Zin found out by series resistor method is 1001.5257 Ω at 10khz
But Zin calculated via plot method (ltspice) i.e Vtest/ Itest is 1909.066 Ω at 10khz for reference

My query is that both the method should yield the same value for Zin.
Why do the Zin values calculated by both methods differ?

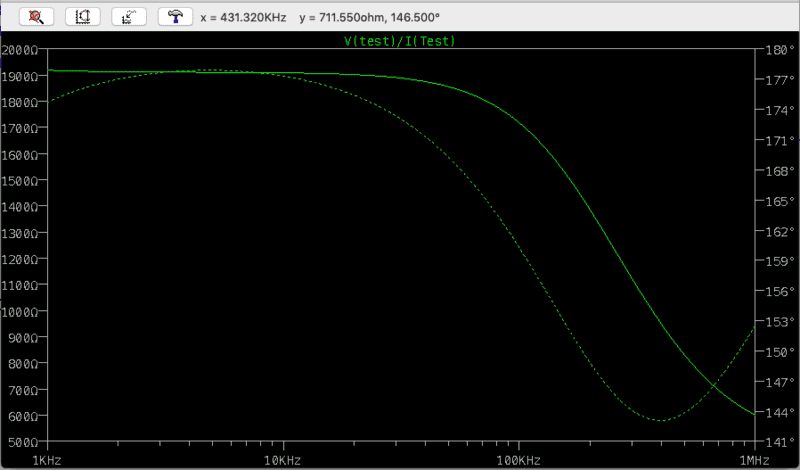
fig- input impedance via Vtest/ Itest (ltspice plot method)

Note: attached are two .asc files which represent the calculation of input impedance using series resistor manual method & plot method i.e Vtest/ I test.


Thanks

 

[Baluncore]

Judging by your power supply polarity, I think the 2N3906 in your files.asc.txt need to be inverted.
Ctrl R twice, followed by ctrl E.
Let us know if that does not make a difference.

 

[brainbaby]

Judging by your power supply polarity, I think the 2N3906 in your files.asc.txt need to be inverted.
Ctrl R twice, followed by ctrl E.

Inverting 2N3906 yield input impedance way out of proportion to 8kΩ
however, inverting the power supply brings the value of input impedance down to 1030Ω or 1.03kΩ around 10khz which seems very much reasonable near to my calculated value of 1001 Ω. Isn't?

 

[Tom.G]

B..B..B..But the OP specified a Common Collector ckt. (Emitter Follower), it is now a Common Emitter ckt.

The original ckt was using the transistor in 'inverted' (? 'inverse') mode, swapping the Emitter and Collector. They can operate that way, but not very well.

No wonder the results were confusing.

 

[Baluncore]

Your first figure shows a common emitter with a crazy bias network, not a CC amplifier.

Your second figure looks better.

I get Zin = 7.1093266 k ohm, no matter how I do it.
Plot "1k0*V(V2)/V(v1,v2)" or "V(V2)/I(Rs)" to get identical results.

Don't forget that the voltages and currents are vectors. You must allow for phase if you do the computation from the magnitude only.

 

[Baluncore]

Here are my LTspice .asc and .plt files.

 

[Baluncore]

If I assume frequency = 10 kHz, and the 2N3906 beta is 200, then compute complex impedance as I work my way from right to left across the ladder diagram, I get; Zin = 7127.45 ohms.
That compares well with LTspice Zin = 7109.3266 ohms.

 

[brainbaby]

1k0*V(V2)/V(v1,v2)

I didn't comprehend this. what does 1k0 signify here?

 

[Baluncore]

The current i, through the 1k0 resistor drops a voltage = i * 1000 = V(V1,V2).
We must divide the V(V1,V2) by 1000 = 1k0 to scale Zin.
Since it is inverse we multiply.

Here is the impedance at 10 kHz, with beta = 193.1

  Impedance       Resistance     Reactance
 Initial RL   (  +1000.000000    +0.000000 j ) ohms
 Series C1    (  +1000.000000    -1.591549 j ) ohms
 Parallel R3  (   +500.000317    -0.397887 j ) ohms
 Beta = 193.1 ( +96550.061141   -76.832000 j ) ohms
 Parallel R1  ( +24593.986082    -4.985338 j ) ohms
 Parallel R2  (  +7109.324214    -0.416575 j ) ohms
 Series C2    (  +7109.324214   -16.332069 j ) ohms
 Magnitude Zin = +7109.342973 ohms
 LTspice   Zin =  7109.3266 ohms

 

[The Electrician]

I didn't comprehend this. what does 1k0 signify here?

1k0 is 1000 ohms. Have a look at: https://en.wikipedia.org/wiki/Common_collector

For a sanity check calculation using figure 3 of the wiki page we have Rin = β*RE for the transistor and RE alone.

Your circuit has R3 = 1000 ohms (1k0) in parallel with RL = 1000 ohms; that gives RE = 500 ohms for the load on the emitter. From that using Rin = β*RE with β ~ 200, we get Rin = 100000 ohms at the base. But the two resistors of the bias network are in parallel with that, so finally Zin of the total circuit is given by
Zin = R1 || R2 || β*RE which is approximately 7127 ohms.