Calculating Length of Arc BD with Hookes Law

[Dell]

in the following question,

E=65 GPa
V=0.3

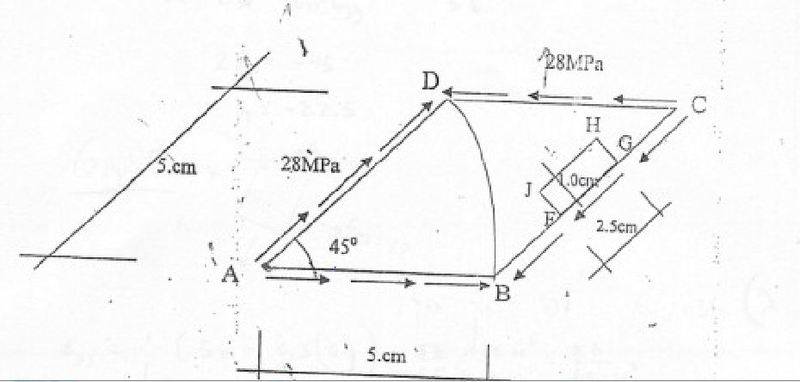
find the new length of the arc BD??

i have found the stresses

$$\sigma$$xx=-56Mpa
$$\sigma$$yy=0
$$\sigma$$xy=-28Mpa

using hookes law i can find the strains

$$\epsilon$$xx=-8.615e-5
$$\epsilon$$yy=2.58e-4
0.5*$$\epsilon$$xy=$$\gamma$$=-1.12e-3

but how do i calculate the change in the arc using this? i would know how to solve this if i had some kind of angular strain- i need to use a polar system not Cartesian. is there any way to do this?

also how do i know the new angle DAB? i know that the XY axis' new angle is 90.06417, and the n,t system (axes tilted 45 degrees to XY) is also 90.06417 but how do i find DAB,? generally is there any way of knowing how the axis is strained, for example, has the X axis dropped 0.06417 degrees, or the Y axis opened up 0.06417 degrees, or a bit each??
in this specific case can i say that since there is no yy strain the x-axis stays at the same angle?

DA*=DA(1+$$\epsilon$$tt)=4.999569cm
AB*=5.0012923cm

 

[Dell]

can i do this:

using the transformation equations, i know

ε_nn= (ε_xx + ε_yy)/2 + (ε_xx - ε_yy)/2*cos(2ϴ) + ε_xxsin(2ϴ)

since i have already found xx, yy, xy, instead of looking for a specific ε_nn can i take the whole eqaution and say

ΔL=$$\int$$ε_nndL {dL=r*dϴ}

=$$\int$$ε_nn*r*dϴ with my integral going from 0 to pi/4

is this a possibility?

 

[Dell]

i tried the following logic,
since in this special specific case, i have found that $$\epsilon$$_xx = $$\epsilon$$_AD, i know that the radiiii will stay rhe same lengths as each other after deformation therefore preserving the circular shape of the arc

knowing that the volume of the shape with an area of an eighth of a circle (DAB) before deformation is V and after deformation is V'
lets say the thickness of the board is "t"

the new angle DAB is " a' " after deformation

$$\Delta$$=($$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)

V=(pi*R²)t/8

V'= (a')(R')²(t')/2

but i also know that

V'=$$\Delta$$*(1+V)
R'=R(1+$$\epsilon$$_xx)
t'=t(1+$$\epsilon$$_zz)

(a')(R')²(t')=(pi*R²)t/8*(1+$$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)

(a')(R(1+$$\epsilon$$_xx))²(t(1+$$\epsilon$$_zz))=(pi*R²)t/8*(1+$$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)therfore i get

(a')= (pi/4)*(1+$$\epsilon$$_xx +$$\epsilon$$_yy + $$\epsilon$$_zz)/[(1+$$\epsilon$$_xx))²((1+$$\epsilon$$_zz))]

once i have the new angle, since it is still an arc of a circle

L'=R'*a'
L=R*pi/4

$$\delta$$L=L'-L

but this gives me an incorrect answer

is this a correct method and do i maybe have something wrong in y calculations

i get $$\delta$$L=1.016463761198405e-005